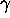In the hand-waving spirit of the preceding Section, let's explore
the consequences of Eq. (
E=mc2.3).
The binomial expansion of
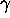is
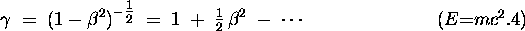
For small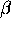 
,
we can take only the first two terms
(later terms have still higher powers of 
and
are considered negligible) to give the approximation
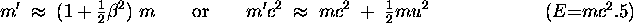
The last term on the right-hand side is what we ordinarily think of as the kinetic energy T. So we can write the equation (in the limit of small velocities) as
It turns out that Eq. ( E=mc2.6) is the exact formula for the kinetic energy at all velocities, despite the ``handwaving'' character of the derivation shown here.
We can stop right there, if we like; but the two terms on the
right-hand side of Eq. (
E=mc2.6) look so simple and similar
that it is hard to resist the urge to give them names and
start thinking in terms of them.
It is conventional to call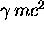 
the total relativistic energy
and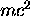 
the rest mass energy.
What do these names mean? The suggestion is that there is
an irreducible energy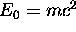 
associated with any object of mass m, even when it is sitting still!
When it speeds up, its total energy changes by a multiplicative
factor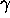 
; the difference
between the total energy
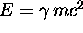and
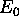is the energy due to
its motion, namely the kinetic energy T.
