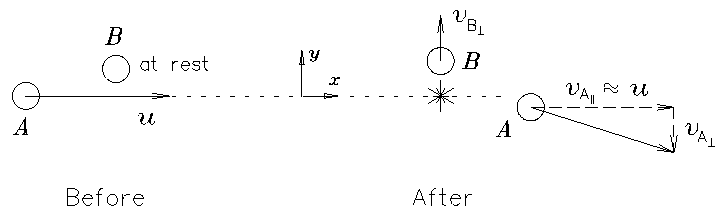
For instance, momentum conservation must still hold, or else we would be able to tell one reference frame from another (in an absolute sense) by seeing which one got less than its share of momentum in a collision. To pursue this example, we invoke momentum conservation in a glancing collision between two identical billiard balls, as pictured below.
Figure:
A glancing collision between two identical billiard balls
of rest mass m. Ball A barely touches ball B
as it passes at velocity u, imparting a miniscule transverse
velocity 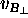 (perpendicular to the initial velocity of A)
to ball B and picking up its own transverse velocity
(perpendicular to the initial velocity of A)
to ball B and picking up its own transverse velocity 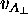 in the process. Unprimed quantities
(like
in the process. Unprimed quantities
(like 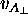 and
and 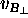 ) are measured in A's reference frame,
whereas primed quantities (like
) are measured in A's reference frame,
whereas primed quantities (like 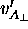 and
and 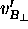 )
are measured in B's reference frame. This drawing is shown in B's
reference frame.
)
are measured in B's reference frame. This drawing is shown in B's
reference frame.
Now, each of A and B measures![]() its own final transverse velocity (relative to the fixed
dotted line along which A was originally travelling)
and sends a message to the other describing the results.
These messages will agree --
its own final transverse velocity (relative to the fixed
dotted line along which A was originally travelling)
and sends a message to the other describing the results.
These messages will agree -- 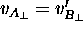 --
but if B measures the final transverse velocity of A
in its (B's) rest frame, namely
--
but if B measures the final transverse velocity of A
in its (B's) rest frame, namely 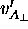 ,
the result will be different due to time dilation.
The logic of this statement is as follows:
,
the result will be different due to time dilation.
The logic of this statement is as follows:
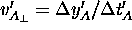 where
where
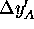 is the distance travelled by A
(perpendicular to its original direction)
in a time
is the distance travelled by A
(perpendicular to its original direction)
in a time 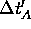 (as seen by B).
Now,
(as seen by B).
Now, 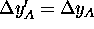 because lengths transverse to
the direction of motion do not differ between reference frames.
On the other hand,
because lengths transverse to
the direction of motion do not differ between reference frames.
On the other hand, 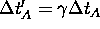 because of
time dilation - the nearly stationary observer on B
measures a longer time interval for processes in the moving frame A
than are observed by A itself.
Since
because of
time dilation - the nearly stationary observer on B
measures a longer time interval for processes in the moving frame A
than are observed by A itself.
Since 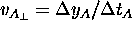 in A's own frame,
this means B ``sees'' a smaller transverse velocity
in A's own frame,
this means B ``sees'' a smaller transverse velocity
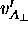 for A than A ``sees'' in its own rest frame
(
for A than A ``sees'' in its own rest frame
(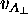 ), by a factor of
), by a factor of 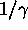 :
:
Meanwhile we must have momentum conservation for the collision.
This means that the transverse momentum of A as observed by B,
namely 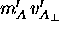 , must be the same as that of B,
namely
, must be the same as that of B,
namely 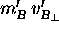 . But the latter transverse velocity
(
. But the latter transverse velocity
(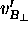 ) is the same as that of A as measured in its own frame
(
) is the same as that of A as measured in its own frame
(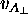 ) and the mass of either ball measured in its own frame
is just the rest mass m, so we have
) and the mass of either ball measured in its own frame
is just the rest mass m, so we have
where you may have noticed that I have started putting subscripts and primes on masses in anticipation of the conclusion
that the only way to reconcile momentum conservation [Eq. (E=mc2.2)] with the relativity of transverse velocity [Eq. (E=mc2.1)] is to treat the mass - or at least the effective mass - as yet another quantity which may have different values when viewed from different reference frames. The result is obtained easily from Eq. (E=mc2.2) and Eq. (E=mc2.1):
where the ``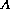 '' subscript has been dropped to make Eq. (E=mc2.3)
more general. In words, it reads
4.5in The effective mass
'' subscript has been dropped to make Eq. (E=mc2.3)
more general. In words, it reads
4.5in The effective mass 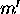 of an object moving at
a velocity
of an object moving at
a velocity 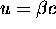 is
is 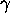 times its rest mass m
(its mass measured in its own rest frame).
That is, moving masses have more inertia!
times its rest mass m
(its mass measured in its own rest frame).
That is, moving masses have more inertia!