


Next: Mass and Energy
Up: Momentum is Still
Previous: Momentum is Still
The preceding argument was not very rigourous, but it served to show
the essential necessity for regarding the effective mass
of an object as a relative quantity.
Let's see what happens as we try to accelerate a mass to the
velocity of light: at first it picks up speed just as we have
been trained to expect by Galileo. But as
But as 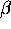 becomes appreciable, we begin to see an interesting
phenomenon: it gets harder to accelerate! (This is, after all,
what we mean by ``effective mass.'') As
becomes appreciable, we begin to see an interesting
phenomenon: it gets harder to accelerate! (This is, after all,
what we mean by ``effective mass.'') As 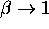 ,
the multiplicative ``mass correction factor''
,
the multiplicative ``mass correction factor'' 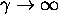 and eventually we can't get any more speed out of it, we just keep
pumping energy into the effective mass. This immediately suggests
a new way of looking at mass and energy, to be developed in the
following Section.
and eventually we can't get any more speed out of it, we just keep
pumping energy into the effective mass. This immediately suggests
a new way of looking at mass and energy, to be developed in the
following Section.
But first let's note an interesting side effect: the rate at which
a constant accelerating force produces velocity changes,
as measured from a nonmoving reference frame,
slows down by a factor 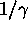 ; but the same factor
governs the time dilation of the ``speed'' of the clock
in the moving frame. So (as observed from a stationary frame)
the change in velocity per tick of the clock in the
moving frame is constant. This has no practical consequences
that I know of, but it is sort of cute.
; but the same factor
governs the time dilation of the ``speed'' of the clock
in the moving frame. So (as observed from a stationary frame)
the change in velocity per tick of the clock in the
moving frame is constant. This has no practical consequences
that I know of, but it is sort of cute.
Jess Brewer
Fri Sep 13 11:17:01 PDT 1996
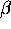 becomes appreciable, we begin to see an interesting
phenomenon: it gets harder to accelerate! (This is, after all,
what we mean by ``effective mass.'') As
becomes appreciable, we begin to see an interesting
phenomenon: it gets harder to accelerate! (This is, after all,
what we mean by ``effective mass.'') As 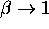 ,
the multiplicative ``mass correction factor''
,
the multiplicative ``mass correction factor'' 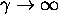 and eventually we can't get any more speed out of it, we just keep
pumping energy into the effective mass. This immediately suggests
a new way of looking at mass and energy, to be developed in the
following Section.
and eventually we can't get any more speed out of it, we just keep
pumping energy into the effective mass. This immediately suggests
a new way of looking at mass and energy, to be developed in the
following Section.
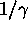 ; but the same factor
governs the time dilation of the ``speed'' of the clock
in the moving frame. So (as observed from a stationary frame)
the change in velocity per tick of the clock in the
moving frame is constant. This has no practical consequences
that I know of, but it is sort of cute.
; but the same factor
governs the time dilation of the ``speed'' of the clock
in the moving frame. So (as observed from a stationary frame)
the change in velocity per tick of the clock in the
moving frame is constant. This has no practical consequences
that I know of, but it is sort of cute.