BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Timing is Everything!
Up: Equations of Motion
Previous: Equations of Motion
Getting back to the subject of Mechanics . . .
One of the reasons the paradigms in the previous chapter emerged
was that physicists were always trying to "solve" certain types
of "problems" using Newton's SECOND LAW,12.4
This equation can be written
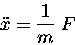 |
(12.1) |
to emphasize that it described a relationship between
the acceleration 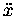 ,
the inertial coefficient m [usually constant]
and the force F.
It is conventional to call an equation in this form
the "equation of motion" governing the problem at hand.
When F is constant [as for "local" gravity]
the "solution" to the equation of motion
is the well-known set of equations governing
constant acceleration, covered in the chapter on FALLING BODIES.
Things are not always that simple, though.
,
the inertial coefficient m [usually constant]
and the force F.
It is conventional to call an equation in this form
the "equation of motion" governing the problem at hand.
When F is constant [as for "local" gravity]
the "solution" to the equation of motion
is the well-known set of equations governing
constant acceleration, covered in the chapter on FALLING BODIES.
Things are not always that simple, though.
Sometimes the problem is posed in such a way that
the force F is explicitly a function of time,
F(t). This is not hard to work with, at least in principle,
since the equation of motion (1) is then in the form
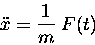 |
(12.2) |
which can be straightforwardly integrated
[assuming one knows a function whose time derivative is F(t)]
using the formal operation
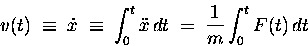 |
(12.3) |
-- which, when multiplied on both sides by m,
leads to the paradigm of Impulse and Momentum.
In other cases the problem may be posed in such a way that
the force F is explicitly a function of position,
F(x). Then the equation of motion has the form
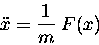 |
(12.4) |
which can be converted without too much trouble
[using the identity
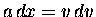 ]
into the paradigm of Work and Energy.
]
into the paradigm of Work and Energy.


Next: Timing is Everything!
Up: Equations of Motion
Previous: Equations of Motion
Jess H. Brewer -
Last modified: Sat Nov 14 12:56:29 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE