BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Mind Your p's and q's!
Up: Exponential Functions
Previous: Exponential Functions
Suppose we have
It is easy to take
the
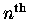 time derivative of this function -
we just "pull out a factor
time derivative of this function -
we just "pull out a factor 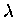 " n times.
For n=2 we get
" n times.
For n=2 we get
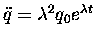 or just
or just
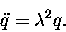 |
(12.10) |
Now go back to the example "solution" in Eq. (5),
which turned out to be equivalent to HOOKES'S LAW
[Eq. (6)]:
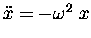 ,
where
,
where
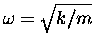 and k and m are the "spring constant" and the mass,
respectively.
and k and m are the "spring constant" and the mass,
respectively.
Equations (10) and (6)
would be the same equation if only we could
let
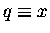 and
and
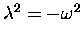 .
Unfortunately, there is no real number whose square is negative.
Too bad. It would be awfully nice if we could
just re-use that familiar exponential function to solve
mass-on-a-spring problems too . . . .
If we just use a little imagination, maybe we can
find a
.
Unfortunately, there is no real number whose square is negative.
Too bad. It would be awfully nice if we could
just re-use that familiar exponential function to solve
mass-on-a-spring problems too . . . .
If we just use a little imagination, maybe we can
find a 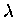 whose square is negative. This would require
having a number whose square is -1, which takes so much
imagination that we might as well call it i.
If there were such a number, then we could just write
whose square is negative. This would require
having a number whose square is -1, which takes so much
imagination that we might as well call it i.
If there were such a number, then we could just write
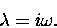 |
(12.11) |
That is, the rate 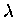 in the exponential formula would have to be an
"imaginary" version of the frequency
in the exponential formula would have to be an
"imaginary" version of the frequency 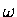 in the oscillatory version, which would mean
(if the solution is to be unique) that
in the oscillatory version, which would mean
(if the solution is to be unique) that
It's not.
Oh well, maybe later . . . .


Next: Mind Your p's and q's!
Up: Exponential Functions
Previous: Exponential Functions
Jess H. Brewer -
Last modified: Sat Nov 14 13:00:04 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE ![]() and
and
![]() .
Unfortunately, there is no real number whose square is negative.
Too bad. It would be awfully nice if we could
just re-use that familiar exponential function to solve
mass-on-a-spring problems too . . . .
If we just use a little imagination, maybe we can
find a
.
Unfortunately, there is no real number whose square is negative.
Too bad. It would be awfully nice if we could
just re-use that familiar exponential function to solve
mass-on-a-spring problems too . . . .
If we just use a little imagination, maybe we can
find a ![]() whose square is negative. This would require
having a number whose square is -1, which takes so much
imagination that we might as well call it i.
If there were such a number, then we could just write
whose square is negative. This would require
having a number whose square is -1, which takes so much
imagination that we might as well call it i.
If there were such a number, then we could just write