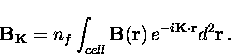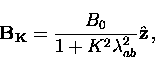


Next: 4.4.1 Vortex Lattice in
Up: 4 Modelling the Internal
Previous: 4.3 Gaussian Field Distribution
A more appropriate way of analyzing the measured field distribution
is to model the contributions to the line shape separately.
The London theory provides the simplest approach to modelling
the internal field distribution n(B) corresponding to the
vortex lattice. The London model
applies exclusively to extreme type II superconductors
in which 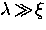 ,
and is independent of the
detailed mechanism responsible for superconductivity.
Furthermore, the London picture is valid at all
temperatures below Tc and for
applied magnetic fields
,
and is independent of the
detailed mechanism responsible for superconductivity.
Furthermore, the London picture is valid at all
temperatures below Tc and for
applied magnetic fields 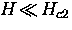 . Both of these
conditions are usually satisfied in
a
. Both of these
conditions are usually satisfied in
a 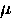 SR experiment.
SR experiment.
For a magnetic field applied in the 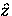 -direction
parallel to the crystallographic
-direction
parallel to the crystallographic 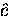 -axis,
the London equation [i.e. Eq. (2.13)]
for the field profile
-axis,
the London equation [i.e. Eq. (2.13)]
for the field profile 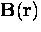 resulting from vortices positioned at the sites
resulting from vortices positioned at the sites 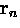 is
is
| ![\begin{displaymath}
{\bf B}({\bf r}) + \lambda_{ab}^2 [ {\bf \nabla} \times
{\bf...
...)]
= \Phi_0 \sum_n \delta ({\bf r} -{\bf r}_n) \hat{\bf z} \, ,\end{displaymath}](img328.gif) |
(6) |
where  ,
,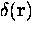 is a two-dimensional delta function and
is a two-dimensional delta function and
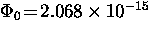 T-m2 is the flux
associated with each vortex.
We restrict the discussion throughout this report to the above mentioned
orientation between the applied magnetic field and the crystal
lattice--hence avoiding
generalizing equations to include the
T-m2 is the flux
associated with each vortex.
We restrict the discussion throughout this report to the above mentioned
orientation between the applied magnetic field and the crystal
lattice--hence avoiding
generalizing equations to include the 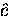 -axis penetration depth.
The points
-axis penetration depth.
The points 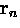 form a two-dimensional periodic lattice in the
form a two-dimensional periodic lattice in the
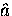 -
-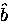 plane, so that
plane, so that 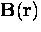 may be expanded in a Fourier series.
The Fourier transform
may be expanded in a Fourier series.
The Fourier transform 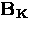 is
is
| 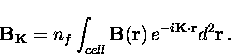 |
(7) |
Here nf is the number of vortices per unit area and 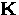 are the reciprocal lattice vectors.
From Eq. (4.6) the Fourier components are
are the reciprocal lattice vectors.
From Eq. (4.6) the Fourier components are
| 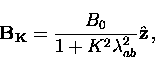 |
(8) |
where 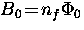 is the average internal field.
Thus the total field at the point
is the average internal field.
Thus the total field at the point 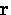 is given by
is given by
Eq. (4.9)
does not account for the finite size of the vortex cores, which are
assumed to be infinitely small--i.e. a delta function is used
as the source term in Eq. (4.6). The spatial dependence
of the order parameter which goes to zero at the center
of the vortex cores is not built into the London theory.
As a result Eq. (4.9) has the unphysical property
that 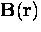 diverges on the axis of the vortex line
at
diverges on the axis of the vortex line
at 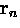 .
To correct for the finite size of the vortex cores,
one can modify Eq. (4.9)
by multiplying each term by a cutoff factor which suppresses
the higher Fourier components
and produces a smooth variation of field to a finite maximum value at
the center of the vortex core.
A sharp cutoff such as at
.
To correct for the finite size of the vortex cores,
one can modify Eq. (4.9)
by multiplying each term by a cutoff factor which suppresses
the higher Fourier components
and produces a smooth variation of field to a finite maximum value at
the center of the vortex core.
A sharp cutoff such as at 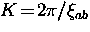 is generally inappropriate because it introduces an oscillatory
cutoff in real space [119].
A smooth cutoff may be obtained by solving the GL equations.
At reduced fields
is generally inappropriate because it introduces an oscillatory
cutoff in real space [119].
A smooth cutoff may be obtained by solving the GL equations.
At reduced fields 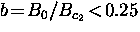 ,Brandt [120] derived the cutoff factor
,Brandt [120] derived the cutoff factor 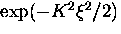 from the isotropic GL theory for
from the isotropic GL theory for 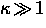 .
At low fields
.
At low fields 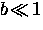 , the cutoff factor is better approximated
by
, the cutoff factor is better approximated
by 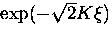 [121].
To account for the field dependence of the order parameter
in GL theory, Brandt also replaces
[121].
To account for the field dependence of the order parameter
in GL theory, Brandt also replaces 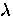 and
and 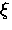 with
with
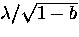 and
and 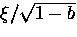 , respectively.
With the external magnetic field applied
parallel to the crystallographic
, respectively.
With the external magnetic field applied
parallel to the crystallographic 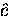 -axis,
the local field at any point in the
-axis,
the local field at any point in the 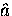 -
-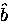 plane is then given by Brandt's modified London model
[54,122,123]
plane is then given by Brandt's modified London model
[54,122,123]
where 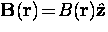 and the
cutoff factor should be replaced with
and the
cutoff factor should be replaced with
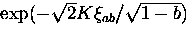 when
when 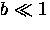 .In Chapter 6,
we shall show that Eq. (4.10) is a
reasonable model for the internal field distribution due to the
vortex lattice in a real superconductor.
.In Chapter 6,
we shall show that Eq. (4.10) is a
reasonable model for the internal field distribution due to the
vortex lattice in a real superconductor.



Next: 4.4.1 Vortex Lattice in
Up: 4 Modelling the Internal
Previous: 4.3 Gaussian Field Distribution
![]() ,
and is independent of the
detailed mechanism responsible for superconductivity.
Furthermore, the London picture is valid at all
temperatures below Tc and for
applied magnetic fields
,
and is independent of the
detailed mechanism responsible for superconductivity.
Furthermore, the London picture is valid at all
temperatures below Tc and for
applied magnetic fields ![]() . Both of these
conditions are usually satisfied in
a
. Both of these
conditions are usually satisfied in
a ![]() SR experiment.
SR experiment.
![]() -direction
parallel to the crystallographic
-direction
parallel to the crystallographic ![]() -axis,
the London equation [i.e. Eq. (2.13)]
for the field profile
-axis,
the London equation [i.e. Eq. (2.13)]
for the field profile ![]() resulting from vortices positioned at the sites
resulting from vortices positioned at the sites ![]() is
is
![\begin{displaymath}
{\bf B}({\bf r}) + \lambda_{ab}^2 [ {\bf \nabla} \times
{\bf...
...)]
= \Phi_0 \sum_n \delta ({\bf r} -{\bf r}_n) \hat{\bf z} \, ,\end{displaymath}](img328.gif)