![[*]](foot_motif.gif) Bardeen et al. [126] later extended the calculations
of Caroli et al. to determine the higher energy scattering
states with
Bardeen et al. [126] later extended the calculations
of Caroli et al. to determine the higher energy scattering
states with
The vortex core in a clean s-wave superconductor was first studied
by Caroli, de Gennes and Matricon [124]. Using a
Bogoliubov formalism these authors calculated
the low-energy spectrum of quasiparticle bound
states in an isolated vortex core in which ![]() ,where
,where ![]() is the bulk energy gap in zero magnetic field.
They determined that the vortex core radius r0 (i.e. where the order
parameter changes appreciably) was on the order
of the coherence length
is the bulk energy gap in zero magnetic field.
They determined that the vortex core radius r0 (i.e. where the order
parameter changes appreciably) was on the order
of the coherence length ![]() .
The model is conceptually the same as the quantum mechanical picture of
a particle in a cylindrical potential well of radius
.
The model is conceptually the same as the quantum mechanical picture of
a particle in a cylindrical potential well of radius
![]() and depth
and depth ![]() .The eigenvalues of the low-lying quasiparticle states may be written as
.The eigenvalues of the low-lying quasiparticle states may be written as
![]() ,
where
,
where ![]() , are the angular momentum quantum
numbers and EF is the Fermi energy.
, are the angular momentum quantum
numbers and EF is the Fermi energy.
![[*]](foot_motif.gif) Bardeen et al. [126] later extended the calculations
of Caroli et al. to determine the higher energy scattering
states with
Bardeen et al. [126] later extended the calculations
of Caroli et al. to determine the higher energy scattering
states with ![]() and the effects of the
magnetic field on the energy of the bound states in the vortex core.
Neumann and Tewordt [127] determined the vortex structure
near Tc by numerically solving the GL equations while various other
authors
obtained vortex-lattice solutions of the Gor'kov microscopic equations
[128,129] near Hc2 using a variety of approximations
[130,131,132,133,134].
and the effects of the
magnetic field on the energy of the bound states in the vortex core.
Neumann and Tewordt [127] determined the vortex structure
near Tc by numerically solving the GL equations while various other
authors
obtained vortex-lattice solutions of the Gor'kov microscopic equations
[128,129] near Hc2 using a variety of approximations
[130,131,132,133,134].
To determine the vortex structure for arbitrary temperature, magnetic field
and impurity concentrations, numerous efforts were made to numerically
solve Eilenberger's equations [135], which are a reformulation
of the microscopic Gor'kov theory.
In the dirty limit the transport-like Eilenberger
equations reduce to the simpler diffusion-like Usadel
equations [136,137].
Using a circular-cell approximation,
Kramer et al. [138] determined the vortex structure
in the dirty limit by numerically solving the Usadel equations near Hc1.
They found that the size of the vortex core shrinks with decreasing T
at low temperatures, but that the effect is much weaker than expected
in the clean limit.
Numerical solutions of the Eilenberger equations for nearly isolated
vortices in the clean limit
were later obtained [139,140], again using
a circular-cell approximation.
In the clean limit the size of the vortex core region was found to shrink
more drastically and the field at the center of the core
increased with decreasing temperature.
In particular, for ![]() the order parameter
the order parameter ![]() and the supercurrent density
and the supercurrent density ![]() are predicted to increase
from the center of an isolated vortex core over a length scale
are predicted to increase
from the center of an isolated vortex core over a length scale ![]() which has a temperature dependence given by [140]
which has a temperature dependence given by [140]
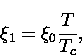 |
(9) |
More recently, Hayashi et al. [148] have investigated
the quantum regime of a single vortex in a clean s-wave superconductor,
by self-consistently solving the Bogoliubov-de-Gennes (BdG) equations.
The temperature dependence of the vortex-core radius is found to
essentially agree with the Kramer-Pesch effect except at temperatures
below the so-called ``quantum limit''. In this limit the temperature
is low enough that
there is no thermal smearing of the discrete bound quasiparticle states
in the vortex cores (i.e. ![]() ). Acccording to
Hayashi et al., the quantum limit is reached below
). Acccording to
Hayashi et al., the quantum limit is reached below
![]() mK in NbSe2. In this temperature region the shrinkage
of the vortex cores must saturate. Unfortunately, experiments thus
far have not probed this low-temperature regime.
mK in NbSe2. In this temperature region the shrinkage
of the vortex cores must saturate. Unfortunately, experiments thus
far have not probed this low-temperature regime.
Scanning tunneling
microscopy (STM) experiments on the
layered hexagonal conventional type-II superconductor NbSe2
by Hess et al. [144] confirmed
the existence of localized states in the cores.
In the vicinity of a single vortex
they measured the differential conductance dI/dV, which is proportional to
the local density of states (LDOS).
Well away from the vortex
center, the dI/dV vs. V scan resembled the standard BCS density of states
for zero magnetic field. In the vortex core region, however, instead of
the constant LDOS expected for the normal state,
they observed a pronounced peak in the differential
conductance centered at zero bias voltage. The peak has been interpreted
as being due to the bound states localized inside the vortex core.
Theoretical efforts [145,146,147,149,150]
shortly followed which focused on calculating the
LDOS observed in this now famous experiment and
subsequent experiments on NbSe2 by
Hess et al. [151,152,153].
In a conventional s-wave superconductor with an isotropic energy
gap, the LDOS has circular symmetry around an isolated vortex core.
Hess et al. observed that the LDOS has a sixfold star shape
around a vortex in NbSe2 [151]. Furthermore, the orientation of the
star was found to depend on the quasiparticle energy and at
intermediate bias voltages the rays split [152].
The origin of the sixfold symmetry in the LDOS
has been explained in terms of vortex-vortex interactions
[154], gap anisotropy [155],
the anisotropic Fermi surface [156], and combinations
of these effects [155].
The magnetic
field distribution ![]() in the vortex core region
will depend on which of these interpretations is correct.
For instance, if vortex-vortex
interactions are the major source then the field distribution
in the vortex core region
will depend on which of these interpretations is correct.
For instance, if vortex-vortex
interactions are the major source then the field distribution
![]() will be nearly circularly symmetric in the vortex core
region and will progress to a definite sixfold symmetry farther away from
the vortex center (as shown in Ref. [154]).
The circular symmetry will extend further out from the vortex center
as the magnetic field is weakened. On the other hand, if the sixfold
symmetry observed in the STM experiments is due to an anisotropic s-wave
energy gap, the sixfold symmetry in
will be nearly circularly symmetric in the vortex core
region and will progress to a definite sixfold symmetry farther away from
the vortex center (as shown in Ref. [154]).
The circular symmetry will extend further out from the vortex center
as the magnetic field is weakened. On the other hand, if the sixfold
symmetry observed in the STM experiments is due to an anisotropic s-wave
energy gap, the sixfold symmetry in ![]() will be more
prominent in the vortex core region. Even in this latter case, however,
the field distribution in the vortex core region can be reasonably
approximated by circular symmetry.
will be more
prominent in the vortex core region. Even in this latter case, however,
the field distribution in the vortex core region can be reasonably
approximated by circular symmetry.
The GL theory has the spatial dependence of the order parameter
built in and thus provides a natural description of the magnetic
field in the vortex-core region.
Abrikosov [157] predicted the vortex state
from his famous periodic solution of the GL equations near Hc2.
He also provided an approximate analytical solution of the GL
equations for an isolated vortex near Hc1. For intermediate
fields, the GL equations must be solved numerically.
The magnetic field distribution obtained from the
exact numerical solutions of the GL equations
coincides with that from the modified London model at low fields and
arbitrary ![]() [158].
J.R. Clem [159] proposed a variational model to solve
the GL equations based upon a trial function for the order parameter:
[158].
J.R. Clem [159] proposed a variational model to solve
the GL equations based upon a trial function for the order parameter:
![]() , where
, where ![]() is a variational
core radius parameter. This model solves the
GL equations approximately at low magnetic fields (i.e. isolated vortices)
yielding an analytical expression for the magnetic field distribution
is a variational
core radius parameter. This model solves the
GL equations approximately at low magnetic fields (i.e. isolated vortices)
yielding an analytical expression for the magnetic field distribution
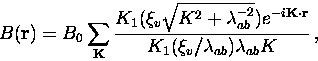 |
(10) |
Hao et al. [160] extended the Clem model to larger magnetic
fields through the linear superposition of the field profiles of
the individual vortices. This included multiplying the trial function
for the order parameter by a second variational parameter ![]() to take into account the depression of the order parameter due to the
overlapping of vortices. In particular,
to take into account the depression of the order parameter due to the
overlapping of vortices. In particular, ![]() as
as
![]() (i.e. the Clem limit) and
(i.e. the Clem limit) and ![]() as B approaches the upper critical field.
Yaouanc et al. [121] recently simplified Hao's
analytical model exclusively to the case of
as B approaches the upper critical field.
Yaouanc et al. [121] recently simplified Hao's
analytical model exclusively to the case of
![]() , where Kmin is the
smallest non-zero reciprocal lattice vector of the vortex lattice.
This condition is satisfied
even at low fields for large
, where Kmin is the
smallest non-zero reciprocal lattice vector of the vortex lattice.
This condition is satisfied
even at low fields for large ![]() superconductors like the high-Tc
compounds. The result is that the local field at any point
in the
superconductors like the high-Tc
compounds. The result is that the local field at any point
in the ![]() -
-![]() plane due to an applied field along the
plane due to an applied field along the
![]() -axis is [121]
-axis is [121]
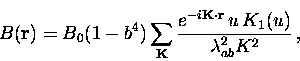 |
(11) |
| |
(12) |
To employ Eq. (4.10) or Eq. (4.13) one must assume an appropriate geometry for the vortex lattice. Theoretically, the equilibrium structure of the vortex lattice can be found by minimizing the Gibbs free energy
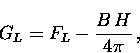 |
(13) |
![\begin{displaymath}
F_L = \int [{\bf h}^2 + \lambda^2 ({\bf \nabla} \times {\bf h})^2] d^2{\bf r}/8
\pi A \, ,\end{displaymath}](img377.gif) |
(14) |
Ideally, the vortex structure is determined by experiment.
This is possible in superconductors which contain few
foreign contaminants or structural defects. For instance,
STM [144,153] and small angle
neutron scattering (SANS) [165] measurements on the
anisotropic conventional type-II superconductor NbSe2
show a perfect triangular lattice with long-range
order, when the magnetic field is
applied parallel to the ![]() -axis.
-axis.