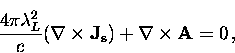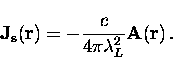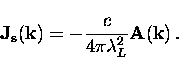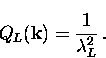


Next: 2.1.2 The BCS Penetration
Up: 2.1 The Magnetic Penetration
Previous: 2.1 The Magnetic Penetration
Let us first consider the magnetic penetration depth
in the context of the conventional
London theory [7] at 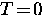 .
If a magnetic field is applied to a superconductor
which is initially in zero field, the magnetic field is a function
of time. According to the Maxwell equation
.
If a magnetic field is applied to a superconductor
which is initially in zero field, the magnetic field is a function
of time. According to the Maxwell equation
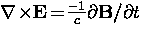 ,the time-varying magnetic field gives rise to an electric field. In a
normal metal this will induce eddy currents, but in a superconductor the
,the time-varying magnetic field gives rise to an electric field. In a
normal metal this will induce eddy currents, but in a superconductor the
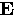 -field will give rise to persistent currents (i.e.
supercurrents).
The induced supercurrents will in turn generate a magnetic field of
their own which opposes the applied magnetic field. If the applied
magnetic field is weak, the flux is totally screened from
the bulk of the superconductor.
This phenomenon is often described as ``perfect diamagnetism''.
From Newton's law, the equation of motion
for a superconducting carrier with mass m and charge -e
in the presence of an electric field
-field will give rise to persistent currents (i.e.
supercurrents).
The induced supercurrents will in turn generate a magnetic field of
their own which opposes the applied magnetic field. If the applied
magnetic field is weak, the flux is totally screened from
the bulk of the superconductor.
This phenomenon is often described as ``perfect diamagnetism''.
From Newton's law, the equation of motion
for a superconducting carrier with mass m and charge -e
in the presence of an electric field 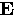 is
is
| 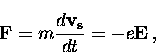 |
(6) |
where 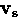 is the velocity of the superconducting carrier.
The field-induced supercurrent density is given by
is the velocity of the superconducting carrier.
The field-induced supercurrent density is given by
| 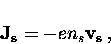 |
(7) |
where ns is the local density of superconducting carriers.
Substituting Eq. (2.7) into Eq. (2.6) gives
| 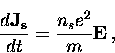 |
(8) |
which is known as the ``first London equation''.
Taking the curl of both sides of Eq. (2.8) gives
| 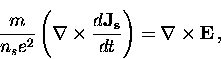 |
(9) |
which can be rewritten using the Maxwell equation
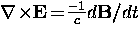 to give
to give
| 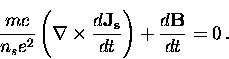 |
(10) |
In order to obtain the Meissner effect (i.e. 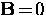 in the
bulk of the superconductor) the London brothers removed the time
derivative in Eq. (2.10) and postulated the new equation
in the
bulk of the superconductor) the London brothers removed the time
derivative in Eq. (2.10) and postulated the new equation
| 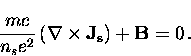 |
(11) |
Equation (2.11) is commonly
referred to as the ``second London equation''.
Since the supercurrent density is related to the
field 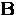 by another Maxwell equation
by another Maxwell equation
| 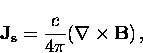 |
(12) |
substitution of Eq. (2.12) into Eq. (2.11) gives
| 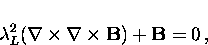 |
(13) |
where
| 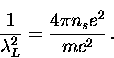 |
(14) |
The variable 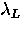 is called the London penetration depth.
Note that
is called the London penetration depth.
Note that 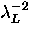 is proportional to the superfluid
density ns.
is proportional to the superfluid
density ns.
The relationship between 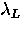 and
and
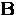 is best realized by a simple example. Consider the
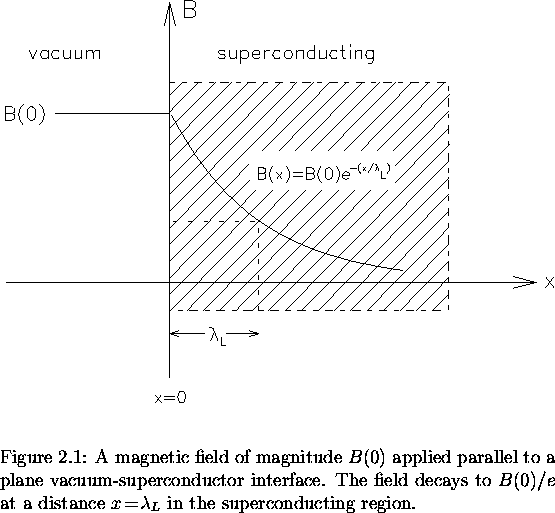
vacuum-superconductor interface illustrated in Fig. 2.1.
If a field
is best realized by a simple example. Consider the
vacuum-superconductor interface illustrated in Fig. 2.1.
If a field 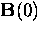 is applied parallel to the surface of the superconductor,
the solution of Eq. (2.13) is
is applied parallel to the surface of the superconductor,
the solution of Eq. (2.13) is
| 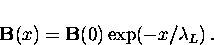 |
(15) |
Thus, both the magnetic field B(x) and the
supercurrent density Js(x) decay exponentially with distance inside
the superconductor over the length scale 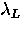 .
.
Equation (2.14) was derived for 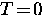 .At nonzero temperature the behaviour of
.At nonzero temperature the behaviour of 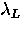 can
be approximated by incorporating the two-fluid model of Gorter
and Casimir [8]. In this model the electron system
is assumed to contain a superconducting component with electron
density ns, and a normal component with an electron density
nn. The total electron density
can
be approximated by incorporating the two-fluid model of Gorter
and Casimir [8]. In this model the electron system
is assumed to contain a superconducting component with electron
density ns, and a normal component with an electron density
nn. The total electron density 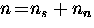 becomes
becomes
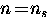 at
at 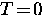 , and
, and
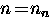 for
for 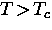 , where Tc is
the superconducting transition temperature.
For arbitrary temperature, Gorter and Casimir found that good
agreement with early experiments could be obtained if one
assumes that
, where Tc is
the superconducting transition temperature.
For arbitrary temperature, Gorter and Casimir found that good
agreement with early experiments could be obtained if one
assumes that ![$n_s (T) \! = \! n[1-(T/T_c)^4]$](img51.gif) .When this expression is combined with Eq. (2.14)
the penetration depth is given by
.When this expression is combined with Eq. (2.14)
the penetration depth is given by
| ![\begin{displaymath}
\lambda_L(T) = \frac{\lambda_L(0)}{\left[ 1-(T/T_c)^4 \right]^{1/2}} \, .\end{displaymath}](img52.gif) |
(16) |
As the temperature T increases, ns is reduced and the magnetic
penetration depth increases with T,
such that 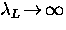 as
as 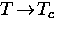 .Although this relation gives a good first-order description
of many of the experimental
results for conventional superconductors, the temperature dependence
is not a prediction from the two-fluid model. Better agreement
is obtained with the behaviour predicted from the
microscopic theory developed by
Bardeen, Cooper and Schrieffer (BCS) [9].
.Although this relation gives a good first-order description
of many of the experimental
results for conventional superconductors, the temperature dependence
is not a prediction from the two-fluid model. Better agreement
is obtained with the behaviour predicted from the
microscopic theory developed by
Bardeen, Cooper and Schrieffer (BCS) [9].
Before considering the BCS theory, let us work backwards to determine
the kernel 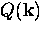 in Eq. (2.2) for the London theory.
The second London equation [i.e. Eq. (2.13)] can be rewritten
using the Maxwell
relation in Eq. (2.12) and the relation
in Eq. (2.2) for the London theory.
The second London equation [i.e. Eq. (2.13)] can be rewritten
using the Maxwell
relation in Eq. (2.12) and the relation
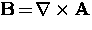 to give
to give
| 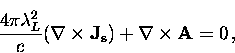 |
(17) |
which is easily solved for 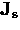 to give
to give
| 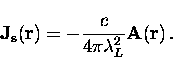 |
(18) |
The 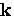 th Fourier component of
th Fourier component of 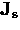 is thus
is thus
| 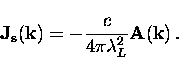 |
(19) |
Comparing Eq. (2.19)
with Eq. (2.2) gives the following simple result for
the London kernel
| 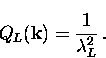 |
(20) |
Clearly, QL is independent of 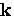 .
This implies that the London theory
is a local theory, where the value of
.
This implies that the London theory
is a local theory, where the value of 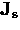 at a point
at a point 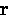 only depends on the value of
only depends on the value of 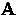 at that same point
at that same point 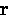 .Generally, the value of
.Generally, the value of 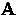 in the
vicinity of the point where
in the
vicinity of the point where 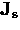 is being measured is
also important. In a more general nonlocal theory,
is being measured is
also important. In a more general nonlocal theory, 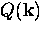 depends
on
depends
on 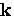 .
.
The current density due to the normal electrons is
| 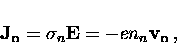 |
(21) |
where 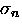 is the finite conductivity of the normal fluid.
Thus, the total current density at arbitrary temperature
below Tc is simply
is the finite conductivity of the normal fluid.
Thus, the total current density at arbitrary temperature
below Tc is simply



Next: 2.1.2 The BCS Penetration
Up: 2.1 The Magnetic Penetration
Previous: 2.1 The Magnetic Penetration
![]() .
If a magnetic field is applied to a superconductor
which is initially in zero field, the magnetic field is a function
of time. According to the Maxwell equation
.
If a magnetic field is applied to a superconductor
which is initially in zero field, the magnetic field is a function
of time. According to the Maxwell equation
![]() ,the time-varying magnetic field gives rise to an electric field. In a
normal metal this will induce eddy currents, but in a superconductor the
,the time-varying magnetic field gives rise to an electric field. In a
normal metal this will induce eddy currents, but in a superconductor the
![]() -field will give rise to persistent currents (i.e.
supercurrents).
The induced supercurrents will in turn generate a magnetic field of
their own which opposes the applied magnetic field. If the applied
magnetic field is weak, the flux is totally screened from
the bulk of the superconductor.
This phenomenon is often described as ``perfect diamagnetism''.
From Newton's law, the equation of motion
for a superconducting carrier with mass m and charge -e
in the presence of an electric field
-field will give rise to persistent currents (i.e.
supercurrents).
The induced supercurrents will in turn generate a magnetic field of
their own which opposes the applied magnetic field. If the applied
magnetic field is weak, the flux is totally screened from
the bulk of the superconductor.
This phenomenon is often described as ``perfect diamagnetism''.
From Newton's law, the equation of motion
for a superconducting carrier with mass m and charge -e
in the presence of an electric field ![]() is
is
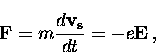
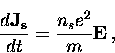
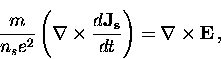
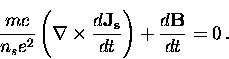
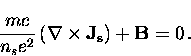
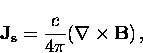
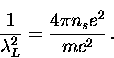
![]() and
and
![]() is best realized by a simple example. Consider the
vacuum-superconductor interface illustrated in Fig. 2.1.
If a field
is best realized by a simple example. Consider the
vacuum-superconductor interface illustrated in Fig. 2.1.
If a field ![]() is applied parallel to the surface of the superconductor,
the solution of Eq. (2.13) is
is applied parallel to the surface of the superconductor,
the solution of Eq. (2.13) is
![]() .At nonzero temperature the behaviour of
.At nonzero temperature the behaviour of ![]() can
be approximated by incorporating the two-fluid model of Gorter
and Casimir [8]. In this model the electron system
is assumed to contain a superconducting component with electron
density ns, and a normal component with an electron density
nn. The total electron density
can
be approximated by incorporating the two-fluid model of Gorter
and Casimir [8]. In this model the electron system
is assumed to contain a superconducting component with electron
density ns, and a normal component with an electron density
nn. The total electron density ![]() becomes
becomes
![]() at
at ![]() , and
, and
![]() for
for ![]() , where Tc is
the superconducting transition temperature.
For arbitrary temperature, Gorter and Casimir found that good
agreement with early experiments could be obtained if one
assumes that
, where Tc is
the superconducting transition temperature.
For arbitrary temperature, Gorter and Casimir found that good
agreement with early experiments could be obtained if one
assumes that ![]() .When this expression is combined with Eq. (2.14)
the penetration depth is given by
.When this expression is combined with Eq. (2.14)
the penetration depth is given by
![\begin{displaymath}
\lambda_L(T) = \frac{\lambda_L(0)}{\left[ 1-(T/T_c)^4 \right]^{1/2}} \, .\end{displaymath}](img52.gif)
![]() in Eq. (2.2) for the London theory.
The second London equation [i.e. Eq. (2.13)] can be rewritten
using the Maxwell
relation in Eq. (2.12) and the relation
in Eq. (2.2) for the London theory.
The second London equation [i.e. Eq. (2.13)] can be rewritten
using the Maxwell
relation in Eq. (2.12) and the relation
![]() to give
to give