


Next: 2.3.2 Nonlinear Effects in dx-y-Wave
Up: 2.3 The Magnetic Field
Previous: 2.3 The Magnetic Field
Since the high-Tc compounds are extreme type-II superconductors,
they should be well described by the London theory.
The underlying assumption in the linear relation between
the supercurrent density 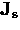 and the vector potential
and the vector potential
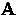 that appears in the London model is that
the applied field is both weak and slowly varying over a distance
that appears in the London model is that
the applied field is both weak and slowly varying over a distance 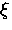 .
This in turn implies that the wave functions of the
superconducting carriers are independent of magnetic field H and
that
.
This in turn implies that the wave functions of the
superconducting carriers are independent of magnetic field H and
that 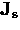 scales exactly with the velocity of the superfluid
scales exactly with the velocity of the superfluid 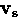 [see Eq. (2.7)].
[see Eq. (2.7)].
Let us first consider an s-wave superconductor in the
Meissner state for the case where 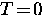 , so that there
is no contribution to
, so that there
is no contribution to 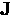 from thermally excited quasiparticles
[i.e. the second term in Eq. (2.22) is zero].
If a static magnetic field is then applied to the BCS ground state,
each electron with initial momentum
from thermally excited quasiparticles
[i.e. the second term in Eq. (2.22) is zero].
If a static magnetic field is then applied to the BCS ground state,
each electron with initial momentum 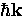 will have a new
momentum given by
will have a new
momentum given by
| 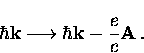 |
(37) |
The other electron in a pair has momentum 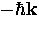 , so
that the new momentum of these electrons is simply
, so
that the new momentum of these electrons is simply
| 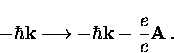 |
(38) |
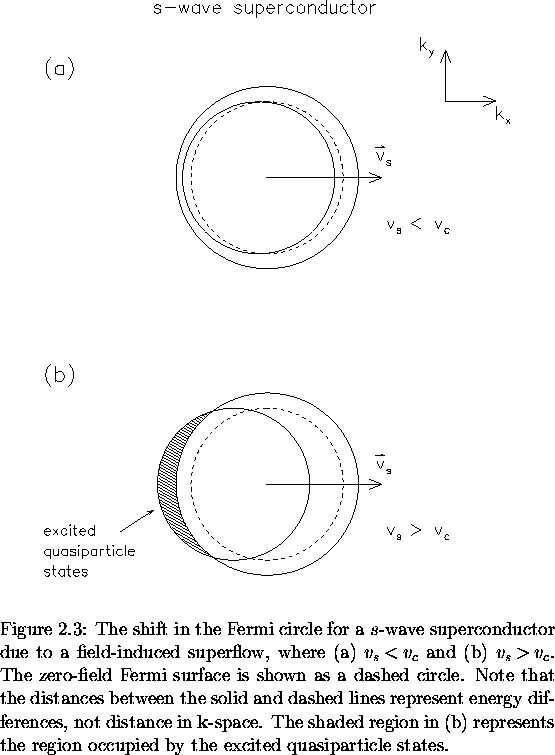
The net effect is to shift the entire Fermi circle in 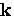 -space
as shown in Fig. 2.3.
-space
as shown in Fig. 2.3.
The change in kinetic energy of an electron pair is
| 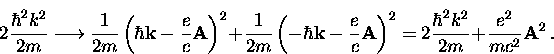 |
(39) |
Using Eq. (2.7) and Eq. (2.18) and summing
up the contribution from all Cooper pairs gives the total increase
in kinetic energy due to the applied magnetic field as
| 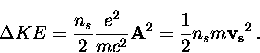 |
(40) |
This is just the classical equation for ns electrons per unit volume
moving with a velocity 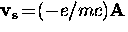 .
Thus, the supercurrents
are determined solely by the applied field, and only exist in its
presence. Provided the displacement of the Fermi circle does not
exceed the width of the energy gap [as in Fig. 2.3(a)],
the supercurrent response will
remain linear. However, if the applied field is large enough, the shift
will exceed this limit and quasiparticle excitations will occur. This latter
case is illustrated in Fig. 2.3(b).
Naturally, this will lead to a reduction in ns and a corresponding
increase in
.
Thus, the supercurrents
are determined solely by the applied field, and only exist in its
presence. Provided the displacement of the Fermi circle does not
exceed the width of the energy gap [as in Fig. 2.3(a)],
the supercurrent response will
remain linear. However, if the applied field is large enough, the shift
will exceed this limit and quasiparticle excitations will occur. This latter
case is illustrated in Fig. 2.3(b).
Naturally, this will lead to a reduction in ns and a corresponding
increase in 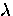 . Near the Fermi surface, a quasiparticle
has kinetic energy
. Near the Fermi surface, a quasiparticle
has kinetic energy 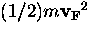 . The change in kinetic energy
of the quasiparticle due
to the superflow velocity
. The change in kinetic energy
of the quasiparticle due
to the superflow velocity 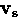 is
is
| 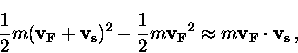 |
(41) |
so that there is a shift in the quasiparticle excitation spectrum such that
| 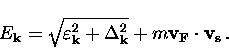 |
(42) |
The shift in quasiparticle energy relative to the energy gap 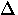 ,can be used to define a critical velocity for vs, below which
the supercurrent response is linear in the
Meissner state of an s-wave superconductor
,can be used to define a critical velocity for vs, below which
the supercurrent response is linear in the
Meissner state of an s-wave superconductor
| 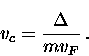 |
(43) |
Thus, if 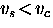 then
then 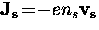 . For
velocities greater than vc, there is a quasiparticle contribution
. For
velocities greater than vc, there is a quasiparticle contribution
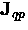 such that the supercurrent density is
such that the supercurrent density is
| 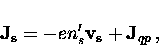 |
(44) |
where 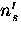 is the reduced value of the superfluid density
(relative to its maximum value ns in the linear regime).
Thus
is the reduced value of the superfluid density
(relative to its maximum value ns in the linear regime).
Thus 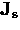 drop rapidly when
drop rapidly when 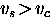 so that the supercurrent response becomes nonlinear.
If the energy shift is larger than the condensation energy (which will
be derived later), the sample will become normal.
so that the supercurrent response becomes nonlinear.
If the energy shift is larger than the condensation energy (which will
be derived later), the sample will become normal.
For 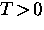 , the size of the energy gap is reduced, so
that the value of vc decreases.
The precise form of the supercurrent-velocity relation
of Eq. (2.45) is [30]
, the size of the energy gap is reduced, so
that the value of vc decreases.
The precise form of the supercurrent-velocity relation
of Eq. (2.45) is [30]
| ![\begin{displaymath}
{\bf J_s} = -e n_s^{\prime}(T) {\bf v_s} \left[1 - \beta_1(T) \left(
\frac{v_s}{v_c} \right)^2 \right] \, ,\end{displaymath}](img139.gif) |
(45) |
where the prefactor 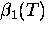 is
a T-dependent coefficient that
decreases rapidly with
T, with
is
a T-dependent coefficient that
decreases rapidly with
T, with 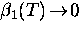 as
as 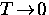 .At low temperatures,
.At low temperatures, 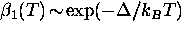 .Using Eq. (2.46), the nonlinear London equations can be
constructed to determine the field dependence of
.Using Eq. (2.46), the nonlinear London equations can be
constructed to determine the field dependence of 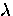 .It is found that for a conventional s-wave superconductor at
low T,
.It is found that for a conventional s-wave superconductor at
low T, 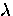 changes quadratically with H
changes quadratically with H
![[*]](foot_motif.gif)
| ![\begin{displaymath}
\frac{\lambda(H,T)}{\lambda(0,T)}
= 1 + \beta_1 (T) \left[ \frac{H}{H_0(T)} \right]^2 \, ,\end{displaymath}](img144.gif) |
(46) |
where 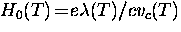 is
a characteristic field on the order of the
thermodynamic critical field Hc(T), which is of course related to vc.
Above H0 (T) the nonlinear effects become important.
The H2 behaviour in Eq. (2.47) has been
confirmed experimentally in the
type-I superconductors Sn and In [31,32,33]
and the type-II superconductor V3Si [34].
The coefficient
is
a characteristic field on the order of the
thermodynamic critical field Hc(T), which is of course related to vc.
Above H0 (T) the nonlinear effects become important.
The H2 behaviour in Eq. (2.47) has been
confirmed experimentally in the
type-I superconductors Sn and In [31,32,33]
and the type-II superconductor V3Si [34].
The coefficient 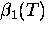 in Eq. (2.47)
is typically small in conventional superconductors.
in Eq. (2.47)
is typically small in conventional superconductors.



Next: 2.3.2 Nonlinear Effects in dx-y-Wave
Up: 2.3 The Magnetic Field
Previous: 2.3 The Magnetic Field
![]() and the vector potential
and the vector potential
![]() that appears in the London model is that
the applied field is both weak and slowly varying over a distance
that appears in the London model is that
the applied field is both weak and slowly varying over a distance ![]() .
This in turn implies that the wave functions of the
superconducting carriers are independent of magnetic field H and
that
.
This in turn implies that the wave functions of the
superconducting carriers are independent of magnetic field H and
that ![]() scales exactly with the velocity of the superfluid
scales exactly with the velocity of the superfluid ![]() [see Eq. (2.7)].
[see Eq. (2.7)].
![]() , so that there
is no contribution to
, so that there
is no contribution to ![]() from thermally excited quasiparticles
[i.e. the second term in Eq. (2.22) is zero].
If a static magnetic field is then applied to the BCS ground state,
each electron with initial momentum
from thermally excited quasiparticles
[i.e. the second term in Eq. (2.22) is zero].
If a static magnetic field is then applied to the BCS ground state,
each electron with initial momentum ![]() will have a new
momentum given by
will have a new
momentum given by
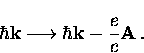
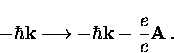
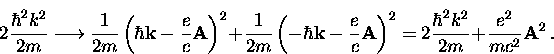
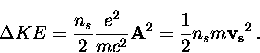
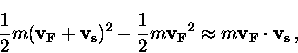
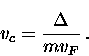
![]() , the size of the energy gap is reduced, so
that the value of vc decreases.
The precise form of the supercurrent-velocity relation
of Eq. (2.45) is [30]
, the size of the energy gap is reduced, so
that the value of vc decreases.
The precise form of the supercurrent-velocity relation
of Eq. (2.45) is [30]
![\begin{displaymath}
{\bf J_s} = -e n_s^{\prime}(T) {\bf v_s} \left[1 - \beta_1(T) \left(
\frac{v_s}{v_c} \right)^2 \right] \, ,\end{displaymath}](img139.gif)
![[*]](foot_motif.gif)
![\begin{displaymath}
\frac{\lambda(H,T)}{\lambda(0,T)}
= 1 + \beta_1 (T) \left[ \frac{H}{H_0(T)} \right]^2 \, ,\end{displaymath}](img144.gif)