For a dx2-y2-wave superconductor,
the presence of nodes on the Fermi surface means that the supercurrent
response to a weak applied magnetic field will be nonlinear even at
![]() . This is clearly seen in Fig. 2.4, where,
due to the nodes, quasiparticle excitations will result from even a
small displacement of the Fermi cylinder. For a given shift, the
precise number of quasiparticle excitations will depend on the
slope of the energy gap function
. This is clearly seen in Fig. 2.4, where,
due to the nodes, quasiparticle excitations will result from even a
small displacement of the Fermi cylinder. For a given shift, the
precise number of quasiparticle excitations will depend on the
slope of the energy gap function ![]() at the
nodes and the direction of
at the
nodes and the direction of ![]() .
The excited quasiparticles located in a narrow wedge at the nodes
produce a current density which flows in a direction opposite
to that of the superfluid.
.
The excited quasiparticles located in a narrow wedge at the nodes
produce a current density which flows in a direction opposite
to that of the superfluid.
For the case in which ![]() is directed along
a node, as shown in Fig. 2.4(a), the supercurrent-velocity
relation is
is directed along
a node, as shown in Fig. 2.4(a), the supercurrent-velocity
relation is
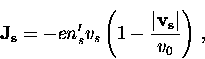 |
(47) |
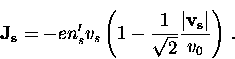 |
(48) |
![\begin{displaymath}
\frac{\lambda(H,T)}{\lambda(0,T)}=1+\beta_2(T)
\left[ \frac{H}{H_0 (T)} \right] \, ,\end{displaymath}](img153.gif) |
(49) |
As the temperature is increased,
there is eventually a crossover to a situation in which thermal excitation of
quasiparticles also occurs away from the nodes.
Below this crossover temperature T*(H),
![]() is linear in H but quadratic
in T, whereas above T*(H),
is linear in H but quadratic
in T, whereas above T*(H), ![]() is quadratic
in H and linear in T [36].
The first evidence for a linear
H-dependence accompanied with a T2-dependence
in a high-Tc material, was obtained by
Maeda et al. [37] for measurements of the in-plane
magnetic penetration depth
is quadratic
in H and linear in T [36].
The first evidence for a linear
H-dependence accompanied with a T2-dependence
in a high-Tc material, was obtained by
Maeda et al. [37] for measurements of the in-plane
magnetic penetration depth ![]() in Bi2Sr2CaCu2Oy.
Similar results have since been reported in YBa2Cu3O
in Bi2Sr2CaCu2Oy.
Similar results have since been reported in YBa2Cu3O![]() and
Tl2Ba2CaCu2Oy [38]. However, the results of
these experiments are suspect because of the large demagnetization effect
(associated with the shape of the sample) which arises from
applying a magnetic field perpendicular to the flat
and
Tl2Ba2CaCu2Oy [38]. However, the results of
these experiments are suspect because of the large demagnetization effect
(associated with the shape of the sample) which arises from
applying a magnetic field perpendicular to the flat
![]() -
-![]() plane.
Early measurements of
plane.
Early measurements of ![]() in a single crystal
of YBa2Cu3O6.95 found a large H2 term [39],
but the sample had a reduced Tc
indicating there may have been extrinsic effects due to impurities.
in a single crystal
of YBa2Cu3O6.95 found a large H2 term [39],
but the sample had a reduced Tc
indicating there may have been extrinsic effects due to impurities.