BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Rigid Bodies
Up: Central Forces
Previous: The Figure Skater
A more formal example of the importance of the Law of
Conservation of Angular Momentum under Central Forces
is in its application to Celestial Mechanics, where
the gravitational attraction of the Sun is certainly a classic
central force. If we always use the Sun as our origin O,
neglecting the influence of other planets and moons,
the orbits of the planets must obey
Conservation of Angular Momentum about the Sun.
Suppose we draw a radius r from the Sun
to the planet in question, as in Fig. 11.6.
Figure:
A diagram illustrating the areal velocity
of an orbit. A planet (mass m) orbits the Sun at a distance r.
the shaded area is equal to
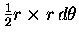 in the limit of infinitesimal intervals [ i.e. as
in the limit of infinitesimal intervals [ i.e. as
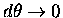 ].
The areal velocity [ rate at which this area is swept out]
is thus
].
The areal velocity [ rate at which this area is swept out]
is thus
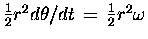 .
.
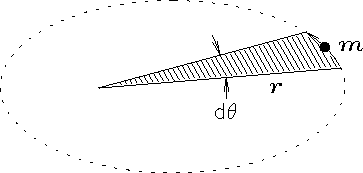 |
The rate at which this radius vector "sweeps out area"
as the planet moves is
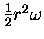 ,
whereas
the angular momentum about the Sun is
,
whereas
the angular momentum about the Sun is
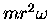 .
The two quantities differ only by the constants
.
The two quantities differ only by the constants 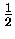 and m; therefore Kepler's empirical observation
that the planetary orbits have constant "areal velocity"
is equivalent to the requirement that the angular momentum
about the Sun be a conserved quantity.
and m; therefore Kepler's empirical observation
that the planetary orbits have constant "areal velocity"
is equivalent to the requirement that the angular momentum
about the Sun be a conserved quantity.


Next: Rigid Bodies
Up: Central Forces
Previous: The Figure Skater
Jess H. Brewer -
Last modified: Sat Nov 14 12:46:28 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE 