BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Kepler Again
Up: Central Forces
Previous: Central Forces
Figure:
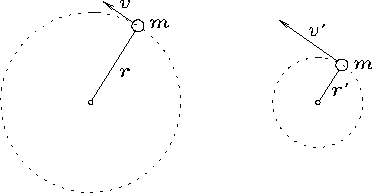
A contrived central-force problem.
The ball swings around (without friction, of course)
on the end of a string fixed at the origin O.
The central force in the string cannot generate
any torque about O, so the angular momentum
LO = m v r
about O must remain constant.
As the string is pulled in slowly, the radius r
gets shorter so the momentum
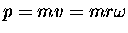 has to increase to compensate.
has to increase to compensate.
 |
Again, so what? Well, there are numerous examples of central forces
in which angular momentum conservation is used to make sense of
otherwise counterintuitive phenomena. For instance, consider the
classic image of the figure skater doing a pirouette:
she starts spinning with hands and feet as far extended as possible,
then pulls them in as close to her body. As a result, even though
no torques were applied, she spins much faster. Why?
I can't draw a good figure skater, so I will resort to a cruder example
[shown in Fig. 11.5]
that has the same qualitative features: imagine a ball (mass m)
on the end of a string that emerges through a hole in an axle
which is held rigidly fixed. The ball is swinging around in a circle
in the end of the string.
For an initial radius r and an initial velocity
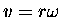 , the initial momentum is
, the initial momentum is
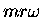 and the angular momentum about O is
and the angular momentum about O is
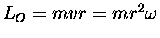 .
Now suppose we
pull in the string until
.
Now suppose we
pull in the string until
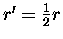 .
To keep the same LO the momentum (and therefore the velocity)
must increase by a factor of 2,
which means that the angular velocity
.
To keep the same LO the momentum (and therefore the velocity)
must increase by a factor of 2,
which means that the angular velocity
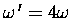 since the ball is now moving at
twice the speed but has only half as far to go around
the circumference of the circle. The period
of the "orbit" has thus decreased by a factor of four!
since the ball is now moving at
twice the speed but has only half as far to go around
the circumference of the circle. The period
of the "orbit" has thus decreased by a factor of four!
Returning to our more æsthetic example of the figure skater,
if she is able to pull in all her mass a factor of 2 closer
to her centre (on average) then she will spin 4 times more
rapidly in the sense of revolutions per second or "Hertz" (Hz).


Next: Kepler Again
Up: Central Forces
Previous: Central Forces
Jess H. Brewer -
Last modified: Sat Nov 14 12:46:10 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE 