BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

Torque and Angular Momentum

Finally we come to the formally trickiest transformation of the SECOND LAW, the one involving the vector product (or "cross product") of   $\mbox{\boldmath$\vec{F}$\unboldmath }$  with the distance   $\mbox{\boldmath$\vec{r}$\unboldmath }$  away from some origin^11.15 "O." Here goes:

$$\mbox{\boldmath $\vec{r}$\unboldmath } \; \times \; \left[ . . . . . . $\unboldmath } \times \mbox{\boldmath $\vec{F}$\unboldmath }$$

Now, the distributive law for derivatives applies to cross products, so

$${d \over dt} \, [ \mbox{\boldmath $\vec{r}$\unboldmath } \tim . . . . . . } \times {d\mbox{\boldmath $\vec{p}$\unboldmath } \over dt}$$

but

$${d\mbox{\boldmath $\vec{r}$\unboldmath } \over dt} \; \equiv . . . . . . h } \; \equiv \; m \, \mbox{\boldmath $\vec{v}$\unboldmath }$$

$$\hbox{\rm so} \qquad {d\mbox{\boldmath $\vec{r}$\unboldmath . . . . . . h } \times \mbox{\boldmath $\vec{v}$\unboldmath }) \; = \; 0$$

because the cross product of any vector with itself is zero.^11.16 Therefore

$${d \over dt} \, [ \mbox{\boldmath $\vec{r}$\unboldmath } \t . . . . . . unboldmath } \times \mbox{\boldmath $\vec{F}$\unboldmath } .$$

If we define two new entities,

$$\mbox{\boldmath$\vec{r}$\unboldmath } \times \mbox{\boldmat . . . . . . math } \; \equiv \; \mbox{\boldmath$\vec{L}$\unboldmath }_O,$$ (11.18)

$$\hbox{\rm the {\sl Angular Momentum\/} about } O$$

and

$$\mbox{\boldmath$\vec{r}$\unboldmath } \times \mbox{\boldmat . . . . . . th } \; \equiv \; \mbox{\boldmath$\vec{\tau}$\unboldmath }_O,$$ (11.19)

$$\hbox{\rm the {\sl Torque\/} generated by } \mbox{\boldmath $\vec{F}$\unboldmath } \hbox{\rm ~about } O \, ,$$

then we can write the above result in the form

$${d \mbox{\boldmath$\vec{L}$\unboldmath }_O \over dt} = \mbox{\boldmath$\vec{\tau}$\unboldmath }_O$$ (11.20)

This equation looks remarkably similar to the SECOND LAW. In fact, it is the rotational analogue of the SECOND LAW. It says that

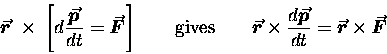
"The rate of change of the angular momentum of a body about the origin  O  is equal to the torque generated by forces acting about  O."

So what? Well, if we choose the origin cleverly this "new" Law gives us some very nice generalizations. Consider for instance an example which occurs very often in physics: the central force.