- . . . potential.1
- In
case this is not self-evident,
remember that the force
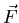 on a charge q is given by
on a charge q is given by
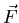 = q
= q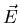 ,
where
,
where 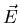 is the electric field,
measured in N/C or V/m. If we move a particle
a distance d
is the electric field,
measured in N/C or V/m. If we move a particle
a distance d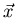 under the influence of a force
under the influence of a force 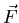 ,
that force does
,
that force does
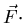 d
d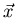 work on the particle
- which appears as kinetic energy!
If we move a charge q=e a distance x
parallel to a constant electric field E,
the work done is e E x,
or (e)(E [V/m])(x [m]) = eV. After all, the reason
work on the particle
- which appears as kinetic energy!
If we move a charge q=e a distance x
parallel to a constant electric field E,
the work done is e E x,
or (e)(E [V/m])(x [m]) = eV. After all, the reason
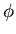 is called the ``electric potential'' is that
when multiplied by q it gives the potential energy of the
charge in the electric field.
is called the ``electric potential'' is that
when multiplied by q it gives the potential energy of the
charge in the electric field.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . kilowatt-hour?2
- Recall
that watts (W) are a unit of
power (energy per unit time) equal to
joules per second: 1 W
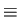 1 J/s.
1 J/s.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . drawings,3
- For
this and the next question, the final result is well known
and the full derivation can be found in any textbook;
however, you will not really own GAUSS' LAW
until you have expressed and used it your own way.
This is true for almost everything, but GAUSS' LAW
is so important (and so simple!) that you should not
miss this chance to make it yours.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.