THE UNIVERSITY OF BRITISH COLUMBIA
Science 1
Physics Assignment # 4:
ELECTRIC CHARGE
26 Jan. 2000 - finish by 02 Feb. 2000
Tipler Ch. 18, problems 25, 33, 34 & 42;
- 1.
- Units:
Moving a charge of one 1 C [one coulomb]
through a potential of 1 V [one volt]
takes 1 J [one joule] of work
(or will produce 1 J of kinetic energy).
This handy relationship is a little clumsy in modern physics,
which deals with elementary particles
whose charge is quantized in units of
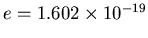 C.
A convenient energy unit in accelerator physics
is therefore the electron volt [eV],
defined as the (kinetic) energy gained by an electron
(or any other particle with the same size charge)
when it is accelerated through a one volt [1 V]
electric potential.1
So . . .
how many electron volts in one kilowatt-hour?2
C.
A convenient energy unit in accelerator physics
is therefore the electron volt [eV],
defined as the (kinetic) energy gained by an electron
(or any other particle with the same size charge)
when it is accelerated through a one volt [1 V]
electric potential.1
So . . .
how many electron volts in one kilowatt-hour?2
- 2.
- Earth's Extra Electrons:
The Earth's atmosphere is a thin electrical insulator
which has an excess of positive charge at higher altitude
an excess of negative charge near the Earth's surface,
which acts like a spherical conductor.
This charge separation gives rise to an approximately constant
electric field pointing down through the atmosphere.
However, above the atmosphere there is no
electric field due to the Earth unless it has a net charge.
Assuming that only electrostatic and gravitational forces are involved,
calculate how many excess electrons the Earth could hold.
(Hint: what will happen to a free electron just outside the atmosphere?)
- 3.
- Gauss' Law for a Sheet of Charge:
Imagine an infinite plane sheet of electric charge
with
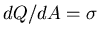 units of charge per unit surface area.
Using your own words and drawings,3
. . .
units of charge per unit surface area.
Using your own words and drawings,3
. . .
- (a)
- Using only (i) the SUPERPOSITION PRINCIPLE
for the total electric field due to an assembly of
electric charges, plus (ii) simple
SYMMETRY arguments, deduce the direction
of the electric field due to the plane of charge.
- (b)
- Using the preceding result plus the general
ideas of GAUSS' LAW and simple geometry,
deduce the dependence of the
magnitude E of the electric field upon x,
the perpendicular distance away from the plane.
- 4.
- Gauss' Law for a Line of Charge:
Imagine an infinite straight line of electric charge
with
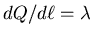 units of charge per unit length.
Using your own words and drawings, . . .
units of charge per unit length.
Using your own words and drawings, . . .
- (a)
- Using only (i) the SUPERPOSITION PRINCIPLE
for the total electric field due to an assembly of
electric charges, plus (ii) simple
SYMMETRY arguments, deduce the direction
of the electric field due to the line of charge.
- (b)
- Using the preceding result plus the general
ideas of GAUSS' LAW and simple geometry
(surface area of a cylinder, etc.),
deduce the dependence of the
magnitude E of the electric field upon r,
the perpendicular distance away from the line.
- 5.
-
Triangle of Charges:
Three charges are placed at the vertices of
an equilateral triangle of side a (as shown)
and a fourth charge is placed at the centre of the triangle.
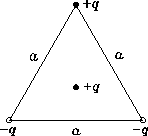
- (a)
- Sketch the electric field lines
inside and outside (nearby) the triangle.
- (b)
- Derive an expression for the vector electric field
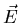 at the centre charge
due to the three other charges at the vertices of the triangle.
at the centre charge
due to the three other charges at the vertices of the triangle.
Jess H. Brewer
2000-01-25

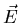 at the centre charge
due to the three other charges at the vertices of the triangle.
at the centre charge
due to the three other charges at the vertices of the triangle.