


Next: The Twin Paradox
Up: No Title
Previous: Simultaneous for Whom?
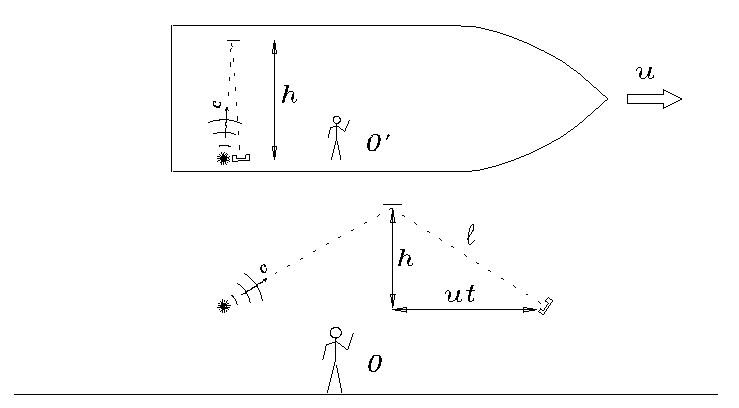
Figure:
A ``light clock" is constructed aboard a glass spaceship
(reference frame O') as follows: the
``tick" of the clock
is defined by one half the time interval t' required
for the light from a strobe light to traverse the width of the ship
(a height h), bounce off a mirror and come back,
a total distance of 2h. In the reference frame of
a ground-based observer O (with respect to whom the ship
is travelling at a velocity u), the light is emitted a
distance 2ut behind the place where it is detected a time
2t later. Since the light has further to go in the
O frame (a distance
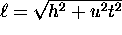 ),
but it travels at c in both frames,
t must be longer than t'.
This effect is known as time dilation.
),
but it travels at c in both frames,
t must be longer than t'.
This effect is known as time dilation.
Fig.  pictures a device used by R.P. Feynman,
among others, to illustrate the phenomenon of time dilation:
a clock aboard a fast-moving vessel (even a normal clock)
appears
pictures a device used by R.P. Feynman,
among others, to illustrate the phenomenon of time dilation:
a clock aboard a fast-moving vessel (even a normal clock)
appears
 to run slower when observed from the ``rest frame"
-- the name we give to the reference frame arbitrarily chosen to
be at rest. Now, if we choose to regard the ship's frame as
``at rest" (as is the wont of those aboard) and the Earth as
``moving," a clock on Earth will appear to be running slowly
when observed from the ship! Who is right?
The correct answer is ``both," in utter disregard for common sense.
This seems to create a logical paradox, which we will discuss
momentarily. But first let's go beyond the qualitative statement,
``The clock runs slower," and ask how much slower.
to run slower when observed from the ``rest frame"
-- the name we give to the reference frame arbitrarily chosen to
be at rest. Now, if we choose to regard the ship's frame as
``at rest" (as is the wont of those aboard) and the Earth as
``moving," a clock on Earth will appear to be running slowly
when observed from the ship! Who is right?
The correct answer is ``both," in utter disregard for common sense.
This seems to create a logical paradox, which we will discuss
momentarily. But first let's go beyond the qualitative statement,
``The clock runs slower," and ask how much slower.
For this we need only a little algebra and geometry;
nevertheless, the derivation is perilous, so watch carefully.
For O', the time interval described in
Fig.  is simply
is simply
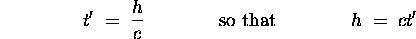
whereas for O the time interval is given by

by the Pythagorean theorem. Expanding the latter equation gives
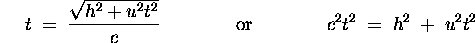
which is not a solution yet because it does not relate
t to t'. We need to ``plug in"
h2 = c2 t'2
from earlier, to get
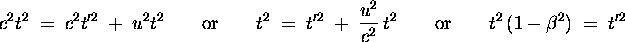
where we have recalled the definition
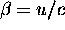 .
In one last step we obtain
.
In one last step we obtain

where 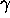 is defined as before:
is defined as before:
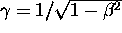 .
.
This derivation is a little crude, but it shows where
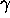 comes from.
comes from.



Next: The Twin Paradox
Up: No Title
Previous: Simultaneous for Whom?
Jess Brewer
Fri Aug 16 17:01:55 PDT 1996

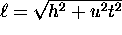 ),
but it travels at c in both frames,
t must be longer than t'.
This effect is known as time dilation.
),
but it travels at c in both frames,
t must be longer than t'.
This effect is known as time dilation.
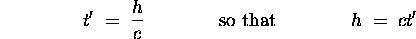

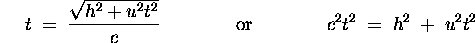
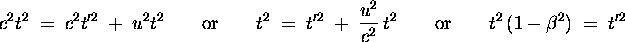
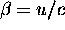 .
In one last step we obtain
.
In one last step we obtain

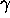 is defined as before:
is defined as before:
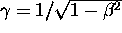 .
.