 with a vector function
with a vector function
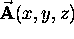 we get a scalar result called the divergence of
we get a scalar result called the divergence of 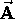 :
:
If we form the scalar (``dot'') product
of  with a vector function
with a vector function
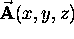 we get a scalar result called the divergence of
we get a scalar result called the divergence of 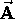 :
:
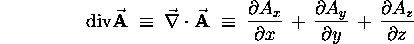
This name is actually quite mnemonic: the divergence of a vector field is a local measure of its ``outgoingness'' --- i.e. the extent to which there is more exiting an infinitesimal region of space than entering it. If the field is represented as ``flux lines'' of some indestructible ``stuff'' being emitted by ``sources'' and absorbed by ``sinks,'' then a nonzero divergence at some point means there must be a source or sink at that position. That is to say,
``What leaves a region is no longer in it.''
For example, consider the divergence of the current density
 , which describes the flux of
a conserved quantity such as electric charge Q.
(Mass, as in the current of a river, would do just as well.)
, which describes the flux of
a conserved quantity such as electric charge Q.
(Mass, as in the current of a river, would do just as well.)
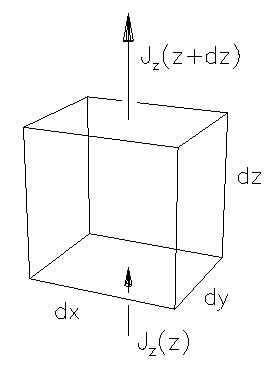
Figure: Flux into and out of a volume element  .
.
To make this as easy as possible, let's picture a cubical
volume element 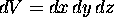 .
In general,
.
In general,  will (like any vector)
have three components
will (like any vector)
have three components 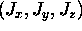 ,
each of which may be a function of position
,
each of which may be a function of position 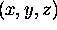 .
If we take the lower left front corner of the cube
to have coordinates
.
If we take the lower left front corner of the cube
to have coordinates 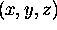 then the upper
right back corner
has coordinates
then the upper
right back corner
has coordinates 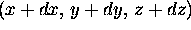 .
Let's concentrate first on
.
Let's concentrate first on 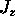 and how it
depends on z.
and how it
depends on z.
It may not depend on z at all, of course.
In this case, the amount of Q coming into the cube
through the bottom surface (per unit time) will be
the same as the amount of Q going out through
the top surface and there will be no net gain or loss
of Q in the volume --- at least not due to 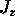 .
.
If 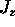 is bigger at the top, however,
there will
be a net loss of Q within the volume dV
due to the ``divergence'' of
is bigger at the top, however,
there will
be a net loss of Q within the volume dV
due to the ``divergence'' of 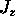 .
Let's see how much: the difference between
.
Let's see how much: the difference between
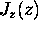 at the bottom and
at the bottom and 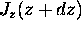 at the top
is, by definition,
at the top
is, by definition,
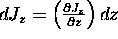 .
The flux is over the same area at top and bottom,
namely
.
The flux is over the same area at top and bottom,
namely 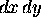 , so the total rate of
loss
of Q due to the z-dependence of
, so the total rate of
loss
of Q due to the z-dependence of 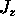 is given by
is given by
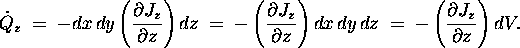
A perfectly analogous argument holds for the x-dependence
if 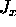 and the y-dependence of
and the y-dependence of
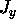 , giving a total
rate of change of Q
, giving a total
rate of change of Q
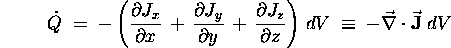
The total amount of Q in our volume element dV
at a given instant is just 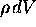 , of
course,
so the rate of change of the enclosed Q is just
, of
course,
so the rate of change of the enclosed Q is just

which means that we can write
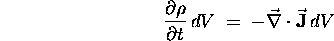
or, just cancelling out the common factor dV on both sides of the equation,

which is the compact and elegant ``differential form'' of the Equation of Continuity.
This equation tells us that the ``Q sourciness''
of each point space is given by the degree to which
flux ``lines'' of  tend to radiate
away
from that point more than they converge toward
that point --- namely, the divergence of
tend to radiate
away
from that point more than they converge toward
that point --- namely, the divergence of  at the point in question. This esoteric-looking mathematical
expression is, remember, just a formal way of expressing
our original dumb tautology!
at the point in question. This esoteric-looking mathematical
expression is, remember, just a formal way of expressing
our original dumb tautology!