- . . . either;1
-
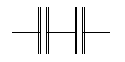
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . either;2
-
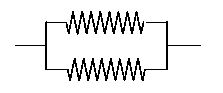
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . either;3
-
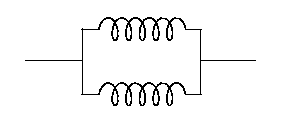
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . either.4
-
This is impossible, of course. Trust your own conclusions!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . particle.5
-
The Lorentz force on a moving charge is
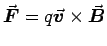 ,
always perpendicular to
,
always perpendicular to
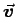 . Thereofre it can only change the
direction of
. Thereofre it can only change the
direction of
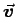 , never its magnitude,
and so
, never its magnitude,
and so 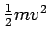 is constant.
is constant.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . C:
6
-
The charge on the capacitor bleeds off through the resistor exponentially:
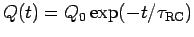 , where
, where 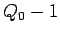 C and
C and
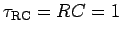 s.
s.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . 7
-
The current in the inductance builds up from zero,
asymptotically approaching the value it would have
without the inductance present, namely
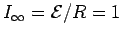 A.
A.
![$I(t) = I_\infty \left[1 - \exp(-t/\tau_{\rm LR})\right]$](img15.gif) , where
, where
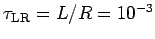 s = 1 ms.
s = 1 ms.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Why?8
-
The increasing upward flux through the loop induces an EMF around the loop
in the direction that will generate its own downward field through
the loop - i.e. clockwise. The force on
the induced current due to the external field is toward the centre
of the loop on both sides, causing it to collapse inward.
Since the loop is a flattened oval, this makes it tend to flatten more.
On the other hand, the fields generated by the induced current
act repulsively on the opposite side of the loop where the current
is going in the opposite direction (opposite currents repel),
so we expect the collapse of the loop to stop when the two
sides get too close together.
If the loop is superconducting, it is not obvious which force
"wins" the battle between attraction and repulsion. This is a
tantalizing problem and gave you a chance to show off the subtlety
of your thinking. Full credit will be given for any answer that
makes sense.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . words.)9
-
Inside the wire,
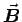 loops around the axis in the sense of the
right hand rule for the inner current. Outside,
loops around the axis in the sense of the
right hand rule for the inner current. Outside, 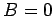 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . cable.10
-
Outside,
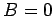 by Ampère's Law because the net current enclosed
by a loop around the cable is zero.
by Ampère's Law because the net current enclosed
by a loop around the cable is zero.
Inside, Ampère's Law gives
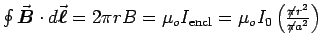 or
or
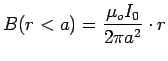 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . .
11
-
The magnetic field is completely contained inside the wire; it makes loops
around the axis and its strength varies with
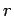 . So we make an area element
. So we make an area element
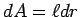 consisting of a long strip of width
consisting of a long strip of width 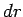 at radius
at radius 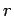 ,
oriented perpendicular to the field. The magnetic flux through this strip is
,
oriented perpendicular to the field. The magnetic flux through this strip is
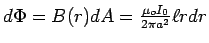 which integrates
easily to give
which integrates
easily to give
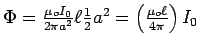 . The definition of
. The definition of 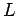 is
is 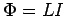 , so
, so
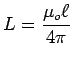 .
The only hard part here is visualizing the geometry for the flux integral.
.
The only hard part here is visualizing the geometry for the flux integral.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . switch.12
-
If a battery was required to "drive" the current in the first place,
then the cable must have a resistance
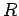 , in which case it constitutes
an
, in which case it constitutes
an 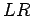 circuit and has a time constant
circuit and has a time constant
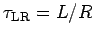 for the exponential decay of the current:
for the exponential decay of the current:
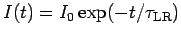 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . cable?13
-
The definition of resistivity can be expressed as
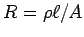 where
where 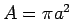 . Thus
. Thus
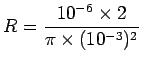 or
or
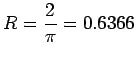
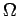 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . conductor?14
-
You can express Ohm's Law either as
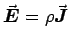 ,
in which case
,
in which case
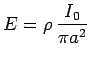 ,
or as
,
or as 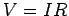 where
where 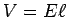 , in which case
, in which case
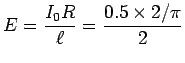 or
or
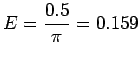 V/m .
V/m .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


![]() or
or
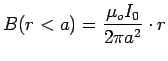 .
.
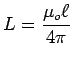 .
The only hard part here is visualizing the geometry for the flux integral.
.
The only hard part here is visualizing the geometry for the flux integral.
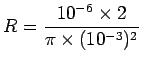 or
or
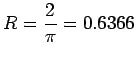
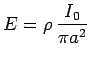 ,
or as
,
or as 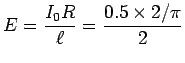 or
or
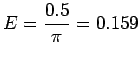 V/m .
V/m .