-
Given only the value of the speed of light,
c = 2.99792458×108 m/s,
and that of the permeability of free space,
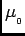 = 4
= 4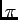 ×10-7 N/A2,
show how to calculate the value of
the permittivity of free space,
×10-7 N/A2,
show how to calculate the value of
the permittivity of free space,
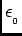 ,
in units of C2/N-m2.
1
,
in units of C2/N-m2.
1
-
The current I in any shorted coil
will exhibit thermal fluctuations.
If a 1 H coil is in thermal equilibrium at a
temperature of 300 K, what is the root mean square current
Irms =
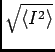 flowing through the coil?
2
flowing through the coil?
2
-
To which of the laws represented by Maxwell's Equations
did Maxwell himself actually make a direct contribution,
and what was his contribution?
3
-
A long straight solenoid of inductance L and resistance R
is made by tightly wrapping one layer of copper conductor
(square cross section, width w) around a circular spindle
of radius r and length
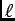 .
If all the dimensions are increased by a factor of 2
(i.e. the picture shown is unchanged
but the scale is doubled),
the time constant of the coil is . . .
4
.
If all the dimensions are increased by a factor of 2
(i.e. the picture shown is unchanged
but the scale is doubled),
the time constant of the coil is . . .
4

[encircle the best answer]
. . . halved. . . . doubled. . . . quartered. . . . quadrupled. . . . unchanged.
(Note: partial credit is possible only if you explain your answer.)
-
Some tropical fish have bright red scales without any red pigments.
Explain briefly how this is possible.
5
-
A proton is initially at rest
in a uniform magnetic field
out of the page, as shown.
A uniform electric field
is then applied in the + y direction,
perpendicular to the magnetic field.
Describe the subsequent motion of the proton qualitatively,
using a simple sketch and a few words.
(Remember, a uniform field is the same everywhere in space.)
6

-
A semi-infinite flat sheet of conductor with thickness d
is viewed "edge-on" at right.
The sheet carries a uniform current density
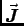 into the page.
Calculate the magnetic field
into the page.
Calculate the magnetic field
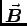 outside the sheet
as a function of
outside the sheet
as a function of
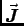 and d.
Explain each step of your reasoning.
7
and d.
Explain each step of your reasoning.
7
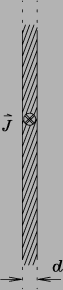
-
An uncharged spherical conducting ball
is suspended by an insulating thread.
A positive point charge is moved near the ball and held fixed.
The ball will . . .
- . . . be attracted to the point charge and swing toward it.
- . . . be repelled from the point charge and swing away from it.
- . . . not be affected by the point charge.
(Note: partial credit is possible only if you explain your answer.)
-
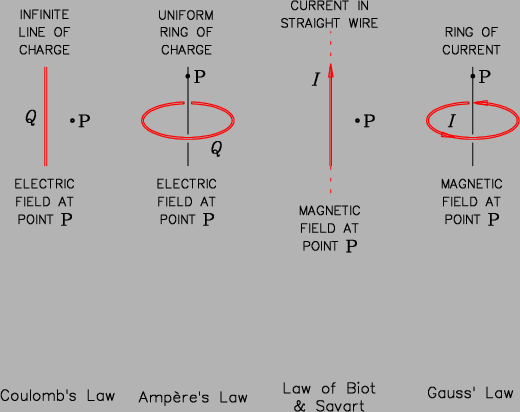
Shown below are four types of calculation problems and four "Laws"
of Electricity and Magnetism. Match up (with connecting lines)
each problem with the Law best suited to solving it.
9
-
An AC power supply produces an oscillating voltage
of 15 V amplitude at 60 Hz.
It is driving a circuit consisting of
a 30
 resistor in series with
a 0.2345 F capacitor and a 30
resistor in series with
a 0.2345 F capacitor and a 30 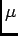 H inductance.
Show that the circuit is being driven on resonance
and then find calculate the maximum current
flowing through the resistor.
10
H inductance.
Show that the circuit is being driven on resonance
and then find calculate the maximum current
flowing through the resistor.
10
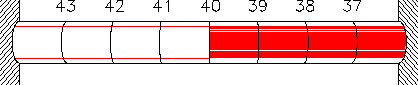
- [3 marks] In what sense is this a "rational" thermometer calibration? 11
- [3 marks] Which end is the bulb on? [Explanation required!] 12
- [4 marks] What is the temperature of the reservoir in degrees Kelvin? 13
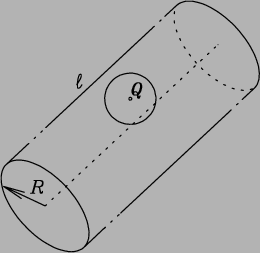
Describe the electric field as a function of position . . .
- [3 marks] . . . in the conductor; 14
- [3 marks] . . . inside the spherical cavity; 15
- [4 marks] . . . outside the conductor (r > R, where r is the perpendicular distance from the cylinder's axis), far fom either end of the cylinder. 16
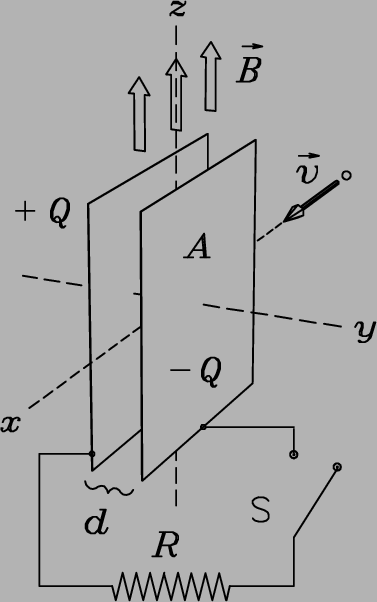
- [3 marks]
For what value of the electric field E
between the plates will the protons pass straight
through without any deflection? 17 - [2 marks] How long will one proton spend inside the velocity selector at that E field? 18
- [5 marks] Calculate the time at which the protons will pass undeflected between the plates. 19
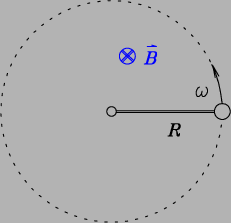
- [2 marks] What is the meaning of the formula
d sin
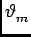 = m
= m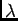 ?
21
?
21
- [2 marks] What is the meaning of the formula
a sin
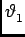 =
= 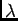 ?
22
?
22
- [2 marks] What is the meaning of the formula
d sin
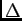
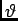 =
= 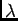 /N ?
23
/N ?
23
- [2 marks] What is the advantage of large N? 24
- [2 marks] How many minima are there between any two adjacent principal maxima? 25