- . . . .
1
- This is partly an exercise in juggling units,
but mainly it requires remembering that
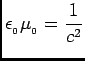 so that
so that
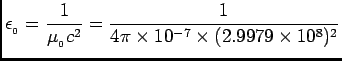 or
or
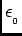 =0.8854×10-11
C2/N . m2 .
=0.8854×10-11
C2/N . m2 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . coil?2
- You must first recognize that this is
a thermal physics problem involving
the equipartition theorem:
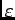
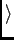 =
= 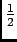 kBT.
Here
kBT.
Here
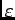 =
= 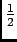 LI2 is the energy stored
in a coil with inductance L carrying current I.
So we have in one step
LI2 is the energy stored
in a coil with inductance L carrying current I.
So we have in one step
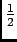 L
L I2
I2 =
=  kBT or
kBT or
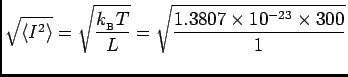 or
Irms = 6.43×10-11 A .
or
Irms = 6.43×10-11 A .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . contribution?3
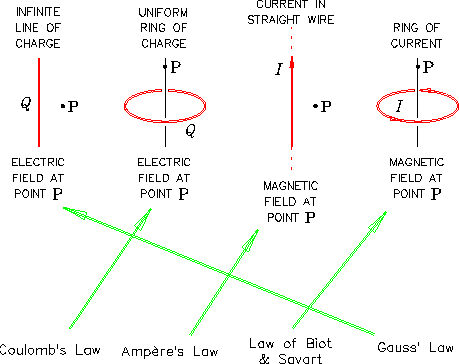
- Maxwell added the displacement current
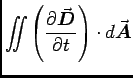 to the right side of Ampère's Law,
to the right side of Ampère's Law,
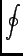
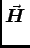 . d
. d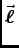 =
=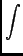
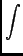
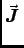 . d
. d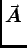 .
(Differential forms are also OK, as are versions with
.
(Differential forms are also OK, as are versions with
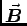 and
and 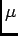 or
or
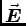 and
and 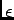 . Just saying the words
was worth full credit.)
. Just saying the words
was worth full credit.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . \dots4
- Let x be the scale factor. We know
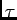 = L/R
so all we need is to deduce the effect on L and R of
x
= L/R
so all we need is to deduce the effect on L and R of
x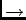 2x. We have
L = NAB/I =
2x. We have
L = NAB/I = 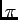 r2
r2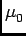 N2/
N2/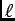
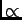 r2/
r2/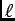
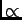 x2/x = x, so L
x2/x = x, so L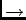 2L
as x
2L
as x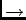 2x. Meanwhile
R =
2x. Meanwhile
R = 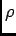
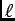 /A
/A 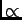 x/x2 = 1/x
so R
x/x2 = 1/x
so R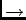 R/2 as x
R/2 as x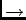 2x. Together these give
2x. Together these give
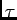
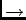 4
4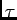 (i.e.
(i.e. 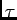 is
quadrupled.
is
quadrupled.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . possible.5
- Thin film interference.
This was meant as a gift. Details are not required,
but the basic idea is that a film of the right thickness
will produce constructive interference between
rays reflected off the front and back sides of the film
if the wavelength is red, and destructive interference
for other wavelengths. Thicker films are more selective,
but harder to grow with sufficient uniformity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . space.)6
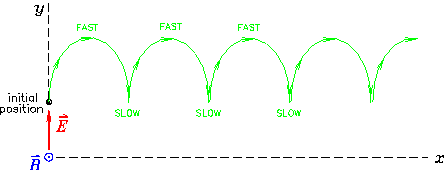
- Something like this:
The initial acceleration is in the + y direction due to
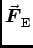 = q
= q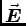 . Once the proton is moving,
. Once the proton is moving,
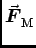 = q
= q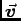 ×
×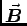 sets in.
Eventually the path must go "horizontal" (in the + x direction)
and then turn around, slow back down due to
sets in.
Eventually the path must go "horizontal" (in the + x direction)
and then turn around, slow back down due to
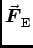 and come back to rest at the same y0 where it started, but
displaced sideways in x. Then the process starts over.
This configuration produces a gradual sideways drift
in the + x direction; it is used in many types of
particle detectors.
and come back to rest at the same y0 where it started, but
displaced sideways in x. Then the process starts over.
This configuration produces a gradual sideways drift
in the + x direction; it is used in many types of
particle detectors.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . reasoning.7
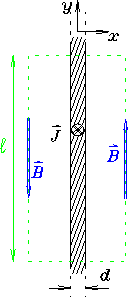
- Obviously we are going to use Ampère's Law,
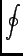
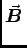 . d
. d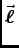 =
=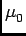 Iencl,
but first we need to make some observations about symmetry:
as long as we stay far away from the ends of the sheet, it
"looks infinite" and there is no way to choose any preferred
value of y. Thus
Iencl,
but first we need to make some observations about symmetry:
as long as we stay far away from the ends of the sheet, it
"looks infinite" and there is no way to choose any preferred
value of y. Thus
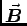 must be independent of y.
When combined with the right hand rule for circulation
of
must be independent of y.
When combined with the right hand rule for circulation
of
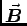 around the current through the rectangular
Ampèrian loop shown below, this implies that
around the current through the rectangular
Ampèrian loop shown below, this implies that
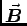 must be along the ±y direction as shown, and
uniform in magnitude. This makes the
line integral trivial: it is just 2B
must be along the ±y direction as shown, and
uniform in magnitude. This makes the
line integral trivial: it is just 2B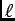 .
The enclosed current is then J times the enclosed area,
or J
.
The enclosed current is then J times the enclosed area,
or J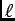 d, giving
2B
d, giving
2B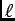 =
= 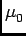 J
J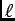 d or
B =
d or
B = 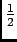
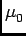 Jd in the directions shown,
independent of y or x (except insofar as it is
up on the right and down on the left.
(Such a device is called a septum magnet.
It is used to split a beam into two parts,
both deflected away from the current sheet.)
Jd in the directions shown,
independent of y or x (except insofar as it is
up on the right and down on the left.
(Such a device is called a septum magnet.
It is used to split a beam into two parts,
both deflected away from the current sheet.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . sentence.]8
- The net charge on the ball is zero, but it is a conductor
and the charges can move. Negative charges will move toward the
positive external charge and pile up on that side, while an equal
amount of positive charge will move toward the far side and pile
up there. This is known as polarizability. In this
configuration, the positive charges in the ball are further
away from the external charge than the negative charges,
and so feel a weaker force; as a result the ball feels a
net attraction to the external charge
and will swing toward it.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . it.9
- Like this:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . resistor.10
- The resonant frequency is
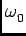 = 1/
= 1/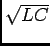 = 1/
= 1/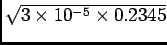 = 377 s-1.
Remember that Hz are cycles per second; to convert
to an angular frequency we must multiply 60 Hz
by 2
= 377 s-1.
Remember that Hz are cycles per second; to convert
to an angular frequency we must multiply 60 Hz
by 2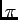 , giving
, giving
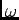 = 2
= 2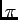 ×60 = 377 s-1.
So we are indeed "on resonance". At this frequency
both L and C "disappear" and the circuit acts as if
we were simply running the driving voltage through the
resistor by itself - in which case
I =
×60 = 377 s-1.
So we are indeed "on resonance". At this frequency
both L and C "disappear" and the circuit acts as if
we were simply running the driving voltage through the
resistor by itself - in which case
I = 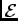 /R
and the amplitude I0 of the current oscillations
is just 15 V divided by 30
/R
and the amplitude I0 of the current oscillations
is just 15 V divided by 30 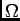 or
I0 = 0.5 A .
or
I0 = 0.5 A .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . calibration?11
- Units of inverse energy are the natural
units for inverse temperature
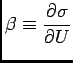 where
where
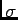
 ln
ln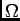 is the dimensionless entropy
and U is the energy of the system. Energy will flow spontaneously
from regions of low
is the dimensionless entropy
and U is the energy of the system. Energy will flow spontaneously
from regions of low 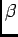 to regions of high
to regions of high 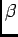 ,
so lower
,
so lower 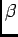 means hotter.
Unlike its inverse, the temperature
means hotter.
Unlike its inverse, the temperature
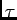
 1/
1/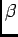 ,
this quantity does not exhibit any divergences where the derivative
goes to zero, and is therefore a more "rational" characterization
of "hotness".
,
this quantity does not exhibit any divergences where the derivative
goes to zero, and is therefore a more "rational" characterization
of "hotness".
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . required!]12
- Judging from the calibration marks, hotter
(lower
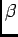 ) is to the right. Thermal expansion
increases as we get hotter, so whatever liquid is expanding
must push the interface away from the bulb
as it gets hotter. This places the bulb on the left.
(The liquid is clear and the red colour on the empty side
is presumably due to some trick of refraction that is spoiled
by the liquid.)
) is to the right. Thermal expansion
increases as we get hotter, so whatever liquid is expanding
must push the interface away from the bulb
as it gets hotter. This places the bulb on the left.
(The liquid is clear and the red colour on the empty side
is presumably due to some trick of refraction that is spoiled
by the liquid.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Kelvin?13
- The thermometer reads 40 eV
-1 =
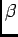 = 1/
= 1/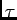 = 1/kBT so
= 1/kBT so
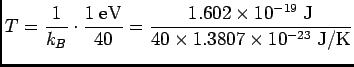 or
T = 290.11 K . A nice comfortable room temperature.
or
T = 290.11 K . A nice comfortable room temperature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . conductor;14
- Zero, as always. This was meant as a gift.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . cavity;15
- By Gauss' Law with spherical symmetry,
field lines originate on + Q at the centre
and drop off radially as 1/
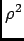 where
where 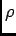 is the distance from the centre of the cavity.
(You can use any symbol you like for this distance, but
not the same one as the distance from the axis of the cylinder.)
When they reach the inner surface of the cavity,
field lines are terminated by induced negative charges
so that none penetrate into the conductor.
Thus
is the distance from the centre of the cavity.
(You can use any symbol you like for this distance, but
not the same one as the distance from the axis of the cylinder.)
When they reach the inner surface of the cavity,
field lines are terminated by induced negative charges
so that none penetrate into the conductor.
Thus
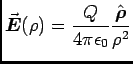 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . cylinder.16
- First you must realize that the positive charges
left behind when - Q is induced on the inner surface of the cavity
will try to get as far away from each other as possible.
They know nothing of the distribution of charges
inside the conductor; all that is shielded by the conductor.
Thus a positive charge + Q is evenly distributed over the
outside of the cylinder. By Gauss' Law with cylindrical symmetry,
this gives the same field outside the cylinder as a long
line of charge with uniform charge per unit length
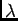 , namely
, namely
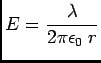 . Finally you must realize that
. Finally you must realize that
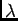 = Q/
= Q/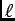 , giving
, giving
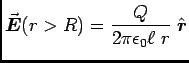 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . deflection?17
-
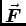 = q(
= q(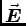 +
+ 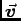 ×
×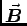 ) = 0
if E = vB in this geometry. Thus the beam passes without
deflection when
E = 106×0.01 = 104 V/m .
) = 0
if E = vB in this geometry. Thus the beam passes without
deflection when
E = 106×0.01 = 104 V/m .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . field?18
- Square plates with area 1 m2 implies a side length
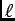 = 1 m. At 106 m/s this takes 10-6 s = 1
= 1 m. At 106 m/s this takes 10-6 s = 1 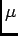 s .
This was partly a gift and partly to avoid confusion about whether
the protons can make it through the separator undeflected
in a time very short compared to the time it takes for the
electric field to change appreciably in the next question.
s .
This was partly a gift and partly to avoid confusion about whether
the protons can make it through the separator undeflected
in a time very short compared to the time it takes for the
electric field to change appreciably in the next question.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . plates.19
- The electric field between the plates is
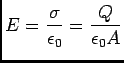 so
E
so
E  Q
and initially
Q
and initially
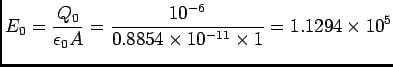 V/m.
For an RC circuit
Q(t) = Q0e-t/
V/m.
For an RC circuit
Q(t) = Q0e-t/ where
where  = RC. Since C = Q/V and V = Ed, we have
= RC. Since C = Q/V and V = Ed, we have
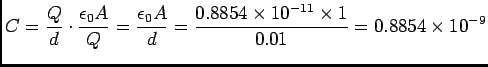 F, giving
F, giving
 = RC = 0.8854×10-9 F
×108
= RC = 0.8854×10-9 F
×108
 = 0.08854 s. We want t such that
= 0.08854 s. We want t such that
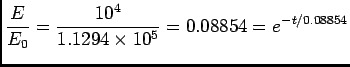 or
ln(0.08854) = - t/0.08854
or
t = 0.21465 s .
or
ln(0.08854) = - t/0.08854
or
t = 0.21465 s .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . negative.20
-
There are at least two valid ways to solve this problem.
One way is to set up a wedge-shaped closed path that goes out
to the ball along the original position of the wire,
along the path followed by the ball, and back to the centre pivot
along the present wire position; then apply Faraday's Law
to the magnetic flux through the path and find the induced
EMF around the loop (which is the voltage across the wire)
at a given instant. The "pie wedge" has an area A
which is in the same ratio to 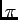 R2 as
R2 as 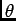 is to 2
is to 2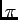 :
A/
:
A/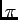 R2 =
R2 = 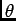 /2
/2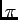 (where
(where
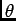 =
= 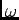 t
is the angle between the original position of the wire
and its current position).
The magnetic flux enclosed by this loop is thus
t
is the angle between the original position of the wire
and its current position).
The magnetic flux enclosed by this loop is thus
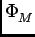 = B
= B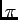 R2
R2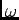 t/2
t/2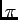 =
= 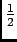
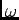 R2Bt
and its time derivative is just
R2Bt
and its time derivative is just
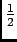
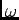 R2B.
Thus
R2B.
Thus
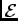 ind = -
ind = - 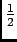
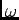 R2B = -
R2B = - 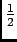 30(0.4)2(0.15) = -0.36 V .
This voltage acts between the ball and the pivot,
the only part of the Faraday loop that is not "virtual".
The downward (into the page) flux through the loop
is increasing as the area of the loop increases,
so by Lenz's Law the induced EMF is in the direction that
would produce a current (if it could) whose magnetic field
would counteract the change in flux - namely a field
upward (out of the page), which would be generated by a
counterclockwise current, which means the ball is
positive and the pivot is negative.
30(0.4)2(0.15) = -0.36 V .
This voltage acts between the ball and the pivot,
the only part of the Faraday loop that is not "virtual".
The downward (into the page) flux through the loop
is increasing as the area of the loop increases,
so by Lenz's Law the induced EMF is in the direction that
would produce a current (if it could) whose magnetic field
would counteract the change in flux - namely a field
upward (out of the page), which would be generated by a
counterclockwise current, which means the ball is
positive and the pivot is negative.
The second approach is to consider the Hall effect
on charges in the wire: a small element of the wire
with length dr at position r < R is moving at a
speed
v = 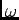 r through the field, producing a
force
F = qvB = q
r through the field, producing a
force
F = qvB = q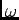 rB which is inward
(toward the pivot) for a positive charge and outward
(toward the ball) for a negative charge. Thus
charges will move in those directions and build up
on the ball or pivot end until an electric field E
is set up (by the charge imbalance) that just cancels
the magnetic force:
qE = q
rB which is inward
(toward the pivot) for a positive charge and outward
(toward the ball) for a negative charge. Thus
charges will move in those directions and build up
on the ball or pivot end until an electric field E
is set up (by the charge imbalance) that just cancels
the magnetic force:
qE = q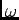 rB or
E =
rB or
E = 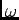 Br.
The voltage between pivot and ball is the integral of
this electric field along the path:
V = -
Br.
The voltage between pivot and ball is the integral of
this electric field along the path:
V = - 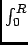 E(r)dr = -
E(r)dr = - 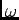 B
B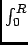 rdr = -
rdr = - 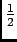
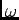 BR2 = -
BR2 = - 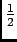 ×30×0.15×(0.4)2 = -0.36 V , in agreement with our
earlier result. The only trouble is, this version
predicts a positively charged pivot and a negatively
charged ball - the opposite of the previous result.
×30×0.15×(0.4)2 = -0.36 V , in agreement with our
earlier result. The only trouble is, this version
predicts a positively charged pivot and a negatively
charged ball - the opposite of the previous result.
Which is right?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ?21
- The angle
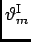 of the
mth
principal maximum of the N-slit interference pattern
is where the phase difference between two adjacent slits
is m(2
of the
mth
principal maximum of the N-slit interference pattern
is where the phase difference between two adjacent slits
is m(2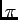 ) and/or the corresponding path difference
is m
) and/or the corresponding path difference
is m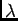 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ?22
- The angle
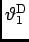 of the first minimum
of the single-slit diffraction envelope
is where the phasors from N "pseudoslits" making up
the slit width all add up to form a closed N-sided
regular polygon with
N
of the first minimum
of the single-slit diffraction envelope
is where the phasors from N "pseudoslits" making up
the slit width all add up to form a closed N-sided
regular polygon with
N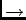
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ?23
- The angular separation
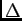
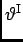 between any principal maximum (PM) of the N-slit
interference pattern and the first minimum
adjacent to that PM is where the phasors from the N slits
add up to form a closed N-sided regular polygon.
between any principal maximum (PM) of the N-slit
interference pattern and the first minimum
adjacent to that PM is where the phasors from the N slits
add up to form a closed N-sided regular polygon.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ?
24
- The width
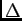
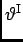 gets smaller
with larger N (see previous formula),
giving sharper principal maxima,
which is especially important when the grating is used to
resolve different colours.
(See Dispersion and Resolving Power.
gets smaller
with larger N (see previous formula),
giving sharper principal maxima,
which is especially important when the grating is used to
resolve different colours.
(See Dispersion and Resolving Power.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . maxima? 25
- N - 1 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
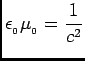 so that
so that
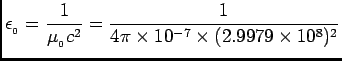 or
or
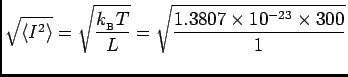 or
Irms = 6.43×10-11 A .
or
Irms = 6.43×10-11 A .
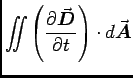 to the right side of Ampère's Law,
to the right side of Ampère's Law,
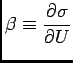 where
where
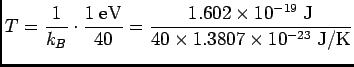 or
T = 290.11 K . A nice comfortable room temperature.
or
T = 290.11 K . A nice comfortable room temperature.
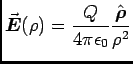 .
.
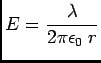 . Finally you must realize that
. Finally you must realize that
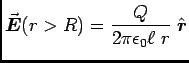 .
.
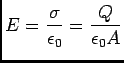 so
E
so
E 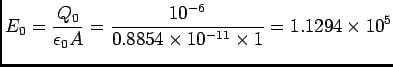 V/m.
For an RC circuit
Q(t) = Q0e-t/
V/m.
For an RC circuit
Q(t) = Q0e-t/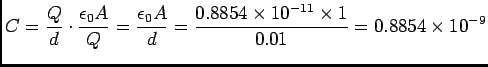 F, giving
F, giving
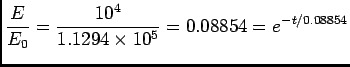 or
ln(0.08854) = - t/0.08854
or
t = 0.21465 s .
or
ln(0.08854) = - t/0.08854
or
t = 0.21465 s .
![]() R2 as
R2 as ![]() is to 2
is to 2![]() :
A/
:
A/![]() R2 =
R2 = ![]() /2
/2![]() (where
(where
![]() =
= ![]() t
is the angle between the original position of the wire
and its current position).
The magnetic flux enclosed by this loop is thus
t
is the angle between the original position of the wire
and its current position).
The magnetic flux enclosed by this loop is thus
![]() = B
= B![]() R2
R2![]() t/2
t/2![]() =
= ![]()
![]() R2Bt
and its time derivative is just
R2Bt
and its time derivative is just
![]()
![]() R2B.
Thus
R2B.
Thus
![]() ind = -
ind = - ![]()
![]() R2B = -
R2B = - ![]() 30(0.4)2(0.15) = -0.36 V .
This voltage acts between the ball and the pivot,
the only part of the Faraday loop that is not "virtual".
The downward (into the page) flux through the loop
is increasing as the area of the loop increases,
so by Lenz's Law the induced EMF is in the direction that
would produce a current (if it could) whose magnetic field
would counteract the change in flux - namely a field
upward (out of the page), which would be generated by a
counterclockwise current, which means the ball is
positive and the pivot is negative.
30(0.4)2(0.15) = -0.36 V .
This voltage acts between the ball and the pivot,
the only part of the Faraday loop that is not "virtual".
The downward (into the page) flux through the loop
is increasing as the area of the loop increases,
so by Lenz's Law the induced EMF is in the direction that
would produce a current (if it could) whose magnetic field
would counteract the change in flux - namely a field
upward (out of the page), which would be generated by a
counterclockwise current, which means the ball is
positive and the pivot is negative.
![]() r through the field, producing a
force
F = qvB = q
r through the field, producing a
force
F = qvB = q![]() rB which is inward
(toward the pivot) for a positive charge and outward
(toward the ball) for a negative charge. Thus
charges will move in those directions and build up
on the ball or pivot end until an electric field E
is set up (by the charge imbalance) that just cancels
the magnetic force:
qE = q
rB which is inward
(toward the pivot) for a positive charge and outward
(toward the ball) for a negative charge. Thus
charges will move in those directions and build up
on the ball or pivot end until an electric field E
is set up (by the charge imbalance) that just cancels
the magnetic force:
qE = q![]() rB or
E =
rB or
E = ![]() Br.
The voltage between pivot and ball is the integral of
this electric field along the path:
V = -
Br.
The voltage between pivot and ball is the integral of
this electric field along the path:
V = - ![]() E(r)dr = -
E(r)dr = - ![]() B
B![]() rdr = -
rdr = - ![]()
![]() BR2 = -
BR2 = - ![]() ×30×0.15×(0.4)2 = -0.36 V , in agreement with our
earlier result. The only trouble is, this version
predicts a positively charged pivot and a negatively
charged ball - the opposite of the previous result.
×30×0.15×(0.4)2 = -0.36 V , in agreement with our
earlier result. The only trouble is, this version
predicts a positively charged pivot and a negatively
charged ball - the opposite of the previous result.