Lorentzian distribution of Lorentzians

As an example of a case where a field-magnitude distribution with no peak at finite 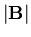$\vert{\bf B}\vert$ is generated by this kind of convolution, let

$$\rho _L(a)=\frac{\textrm{w}}{2\pi }\left( \frac 1{a^2+\textrm{w}^2}\right)$$

be convoluted with a Lorentzian distribution at each site:

$$\begin{array}{c} P_{LL}(B_i)= \frac{(norm)\ln \left( \frac{B . . . . . . t( \frac{B^2}{\textrm{w}^2}-1\right) }\right] . \end{array}$$

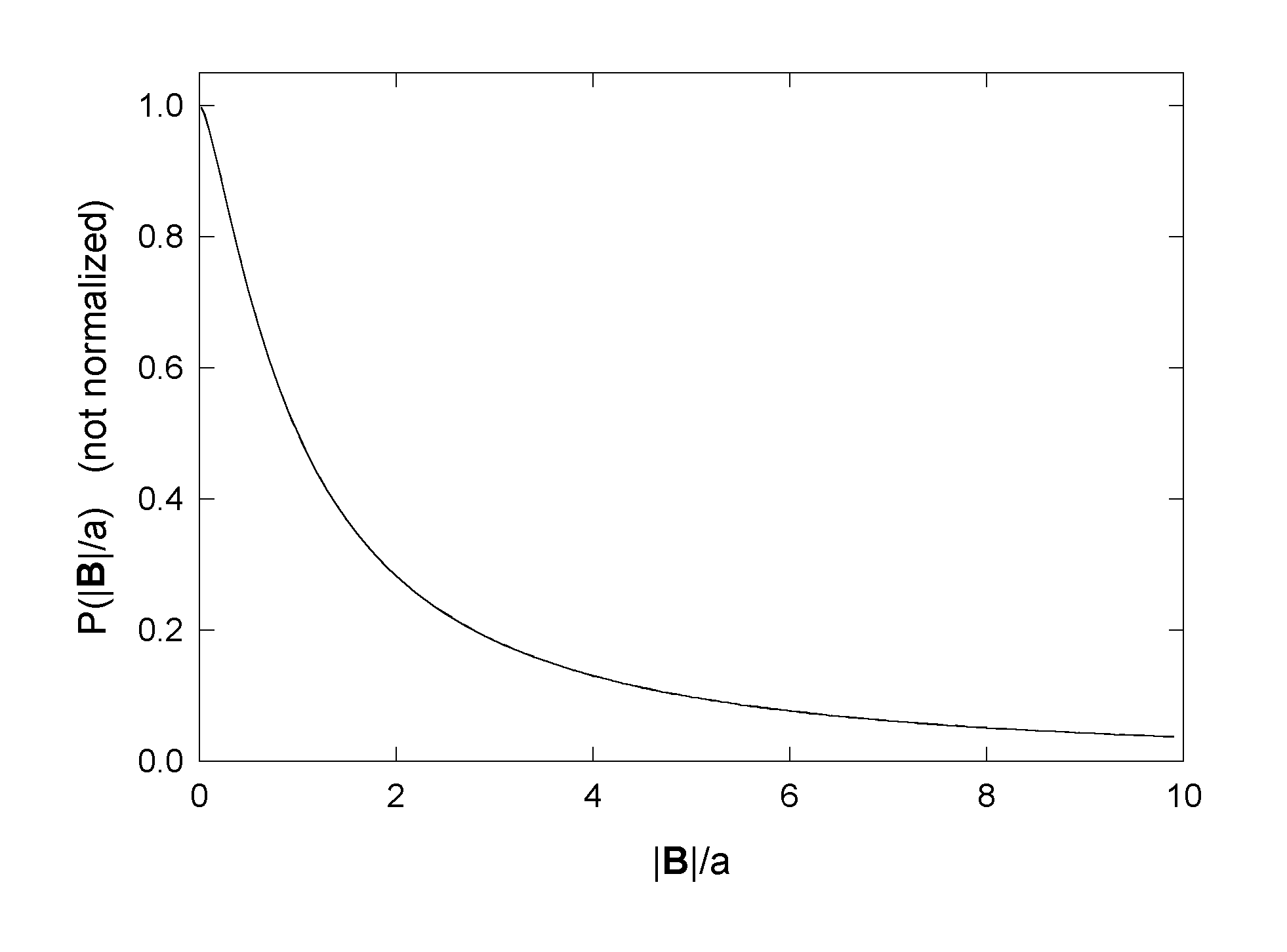
In spite of these expressions not being well defined when B_i=w or B=w, these distributions are smooth through those values. 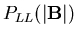$P_{LL}(\vert{\bf B}\vert)$ is shown in Fig.5. Note that it is finite, nonzero at B=0. The corresponding relaxation function is expressible in sine-integral and cosine-integral functions.

Figure 5: