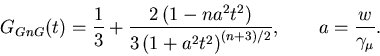

Next: Lorentzian distribution of Lorentzians
Up: Uemura's Site-Distribution Trick
Previous: A different way to go from Gaussian toward
Consider the distribution of site classes:
(n=0 is simply Gaussian) convoluted with a Gaussian field distribution for
each class:
Closed forms can be found for small odd integer n:
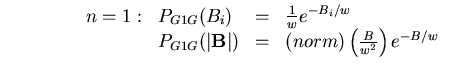
![$\qquad \qquad
\begin{array}[t]{llll}
n=3: & P_{G3G}(B_i) & = & \frac{(norm)} . . .
. . . {\bf B}\vert) & = & (norm)\left( \frac{B^2}{w^3}\right) e^{-B/w}
\end{array}
$](img36.gif)
and static ZF relaxation functions for all n:
This is plotted for small n in Fig.4. Note that while
GGnG(t) always
has zero slope as
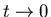 ,
as is proper for a static ZF relaxation
function caused by a field distribution with finite second moment, for small
values of n the minimum is shallower than for the static Lorentzian
Kubo-Toyabe, and
GG0G(t) has Pearson b=3/2 shape, that is, monotonic
relaxation with no minimum at all. This suggests that
,
as is proper for a static ZF relaxation
function caused by a field distribution with finite second moment, for small
values of n the minimum is shallower than for the static Lorentzian
Kubo-Toyabe, and
GG0G(t) has Pearson b=3/2 shape, that is, monotonic
relaxation with no minimum at all. This suggests that
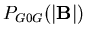 has its maximum value at
has its maximum value at
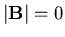 and has no peak at finite field value
(see below).
The distributions of site classes above in this section all peaked at zero: the most
likely value of
and has no peak at finite field value
(see below).
The distributions of site classes above in this section all peaked at zero: the most
likely value of 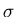 is zero. In a variation of the idea of this section,
a Gaussian (n=0) distribution of site classes peaked around a positive value
is zero. In a variation of the idea of this section,
a Gaussian (n=0) distribution of site classes peaked around a positive value 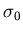 was convoluted with a Gaussian field distribution for each class to produce the
"Gaussian-broadened Gaussian'' relaxation function which applies to some
highly-disordered magnetic materials.[3]
was convoluted with a Gaussian field distribution for each class to produce the
"Gaussian-broadened Gaussian'' relaxation function which applies to some
highly-disordered magnetic materials.[3]
Figure 4:


Next: Lorentzian distribution of Lorentzians
Up: Uemura's Site-Distribution Trick
Previous: A different way to go from Gaussian toward
Jess H. Brewer
2002-09-24
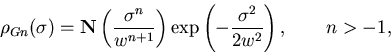
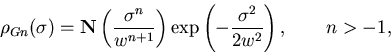
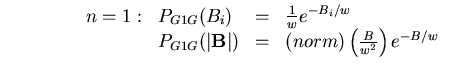
![$\qquad \qquad
\begin{array}[t]{llll}
n=3: & P_{G3G}(B_i) & = & \frac{(norm)} . . .
. . . {\bf B}\vert) & = & (norm)\left( \frac{B^2}{w^3}\right) e^{-B/w}
\end{array}
$](img36.gif)