![]() Vector Notation: a vector quantity is one that has
both magnitude and direction. Another (equivalent)
way of putting it is that a vector quantity has several components
in orthogonal (perpendicular) directions.
The idea of a vector is very abstract and general;
one can define useful vector spaces of many sorts,
some with an infinite number of orthogonal basis vectors,
but the most familiar types are simple 3-dimensional quantities
like position, speed, momentum and so on. The conventional
notation for a vector is
Vector Notation: a vector quantity is one that has
both magnitude and direction. Another (equivalent)
way of putting it is that a vector quantity has several components
in orthogonal (perpendicular) directions.
The idea of a vector is very abstract and general;
one can define useful vector spaces of many sorts,
some with an infinite number of orthogonal basis vectors,
but the most familiar types are simple 3-dimensional quantities
like position, speed, momentum and so on. The conventional
notation for a vector is ![]() ,
sometimes written
,
sometimes written
![]() or
or ![]() or A but most clearly recognizable when in boldface
with a little arrow over the top. On the blackboard a vector
may be written with a tilde underneath, which is hard to
generate in LATEX.
or A but most clearly recognizable when in boldface
with a little arrow over the top. On the blackboard a vector
may be written with a tilde underneath, which is hard to
generate in LATEX.
![]() Unit Vectors:
In Cartesian coordinates (x,y,z) a vector
Unit Vectors:
In Cartesian coordinates (x,y,z) a vector ![]() can be
expressed in terms of its three scalar components
Ax,Ay,Az
and the corresponding unit vectors
can be
expressed in terms of its three scalar components
Ax,Ay,Az
and the corresponding unit vectors
![]() (sometimes written as
(sometimes written as
![]() or occasionally
as
or occasionally
as
![]() )
thus:
)
thus:
A unit vector ![]() can be formed from
any vector
can be formed from
any vector ![]() by dividing it by its own magnitude a:
by dividing it by its own magnitude a:
| (2) |
Already we have used a bunch of concepts before defining them properly, the usual chicken-egg problem with mathematics. Let's try to catch up:
![]() Multiplying or Dividing a Vector by a Scalar:
Multiplying a vector
Multiplying or Dividing a Vector by a Scalar:
Multiplying a vector ![]() by a scalar b has no effect
on the direction of the result (unless b=0)
but only on its magnitude and/or the units
in which it is measured - if b is a pure number,
the units stay the same; but multiplying a velocity by a mass
(for instance) produces an entirely new quantity,
in that case the momentum.
by a scalar b has no effect
on the direction of the result (unless b=0)
but only on its magnitude and/or the units
in which it is measured - if b is a pure number,
the units stay the same; but multiplying a velocity by a mass
(for instance) produces an entirely new quantity,
in that case the momentum.
Dividing a vector by a scalar c is the same as multiplying it by 1/c.
This type of product always commutes:
![]() .
.
![]() Adding or Subtracting Vectors:
In two dimensions one can draw simple diagrams depicting
"tip-to-tail" or "parallelogram law" vector addition
(or subtraction); this is not so easy in 3 dimensions,
Adding or Subtracting Vectors:
In two dimensions one can draw simple diagrams depicting
"tip-to-tail" or "parallelogram law" vector addition
(or subtraction); this is not so easy in 3 dimensions,
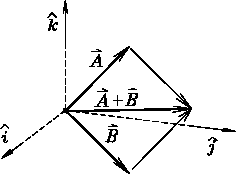
so we fall back on the algebraic method of adding components.
Given ![]() from Eq. (1) and
from Eq. (1) and
![]() Multiplying Two Vectors . . .
Multiplying Two Vectors . . .
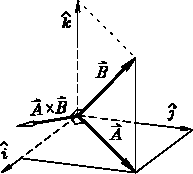
We are going to be using these things continually throughout the rest of the course, so make sure you are adept with them.