BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

Refraction

Figure: Refraction of a wave at a boundary between two media where the propagation velocity ($c$) of the wave in the first medium is greater than that ($c'$) in the second medium. The diagram on the left shows the wavefronts ("crests" of the waves) and the corresponding perpendicular wavevectors $\Vec{k}$ (incoming wave), $\Vec{k}'$ (transmitted wave) and (reflected wave). The diagram on the right shows the angles between the wavevectors and the normal to the interface.

Figure: Refraction of a wave at a boundary between two media where the propagation velocity ($c$) of the wave in the first medium is less than that ($c'$) in the second medium.

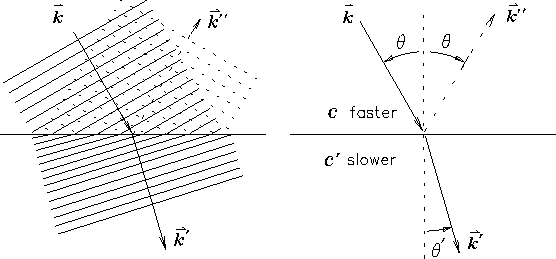
When a wave crosses a boundary between two regions in which its velocity of propagation has different values, it "bends" toward the region with the slower propagation velocity. The following mnemonic image can help you remember the qualitative sense of this phenomenon, which is known as REFRACTION: picture the wave front approaching the boundary as a yardstick moving through some fluid in a direction perpendicular to its length. If one end runs into a thicker fluid first, it will "drag" that end a little so that the trailing end gets ahead of it, changing the direction of motion gradually until the whole meter stick is in the thicker fluid where it will move more slowly.^14.18

Conversely, if one end emerges first into a thinner fluid (where it can move faster) it will pick up speed and the trailing end will fall behind. This picture also explains why there is no "bending" if the wave hits the interface normally (at right angles). The details are revealed mathematically (of course) in SNELL'S LAW:^14.19

$${\sin(\theta) \over \sin(\theta')} = {c \over c'}$$ (14.42)

where $\theta$ is the angle of incidence of the incoming wave (the angle that $\Vec{k}$ makes with the normal to the interface), $\theta'$ is the angle that the refracted wavevector $\Vec{k}'$ makes with the same normal, $c$ is the propagation velocity of the wave in the first medium and $c'$ is the propagation velocity of the wave in the second medium.

Another semi-obvious consequence of the fact that the "crests" of the waves remain continuous^14.20is that the wavelength gets shorter as the wave enters the "thicker" medium or longer as it enters a "thinner" medium. Another way of putting this is that the frequency stays the same (and therefore so does the period $T$) as the wave crosses the boundary. Since $c = \lambda / T$ this means that if the velocity decreases, so does the wavelength. One can follow this argument a bit further to derive SNELL'S LAW from a combination of geometry and logic. I haven't done this, but you might want to . . . .

There is also always a reflected wave at any interface, though it may be weak. The reflected wave is shown as dotted lines in Figs. 14.10 and 14.11, where its wavevector is denoted . This phenomenon is familiar as a source of annoyance to anyone who has tried to watch television in a room with a sunny window facing the TV screen. 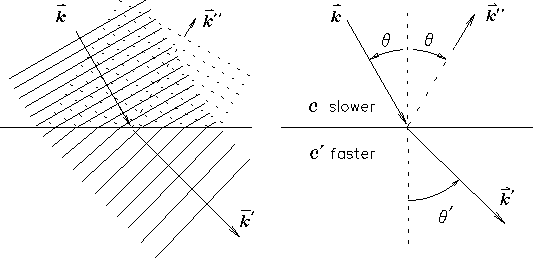However, it does have some redeeming features, as can be deduced from a thoughtful analysis of Eq. (42). For instance, if the wave is emerging from a "thick" medium into a "thin" medium as in Fig. 14.11 (like light emerging from glass into air), then there is some incoming angle $\theta_c$, called the CRITICAL ANGLE, for which the refracted wave will actually be parallel to the interface - i.e. $\theta' = \pi/2$ (90$^\circ$). This implies $\sin(\theta') = 1$ so that SNELL'S LAW reads

$$\sin(\theta_c) \; = \; {c \over c'}$$ (14.43)

which has a solution only if $c' > c$ - i.e. for emergence into a "thinner" medium with a higher wave propagation velocity, as specified earlier.

What happens, qualitatively, is that as $\theta$ gets larger and larger (closer and closer to "grazing incidence") the amplitude (strength) of the transmitted wave gets weaker and weaker, while the amplitude of the reflected wave gets stronger and stronger, until for incoming angles $\theta \ge \theta_c$ there is no transmitted wave and the wave is entirely reflected. This phenomenon is known as TOTAL INTERNAL REFLECTION and has quite a few practical consequences.

Because of total internal reflection, a fish cannot see out of the water except for a limited "cone" of vision overhead bounded by the critical angle for water, which is about $\sin^{-1}(1/1.33)$ or 49$^\circ$. Lest this lend reckless abandon to fishermen, it should be kept in mind that the light "rays" which appear to come from just under 49$^\circ$ from the vertical are actually coming from just across the water's surface, so the fish has a pretty good view of the surrounding environment - it just looks a bit distorted. To observe this phenomenon with your own eyes, put on a good diving mask, carefully slip into a still pool and hold your breath until the surface is perfectly calm again. Looking up at the surface, you will see the world from the fish's perspective (except that the fish is probably a good deal less anoxic) - inside a cone of about 49$^\circ$ from the vertical, you can see out of the water; but outside that cone, the surface forms a perfect mirror!

How total is total internal reflection? Total! If the surface has no scratches etc., the light is perfectly reflected back into the denser medium. This is how "light pipes" work - light put into one end of a long Lucite rod will follow the rod through bends and twists (as long as they are "gentle" so that the light never hits the surface at less than the critical angle) and emerge at the other end attenuated only by the absorption in the Lucite itself. Even better transmission is achieved in FIBER OPTICS, where fine threads of special glass are prepared with extremely low absorption for the wavelengths of light that are used to send signals down them. A faint pulse of light sent into one end of a fiber optic transmission line will emerge many kilometers down the line with nothing "leaking out" in between. (This feature is especially attractive to those who don't want their conversations bugged, or so I am told.) Another application was invented by Lorne Whitehead while he was a UBC Physics graduate student: by an ingenious trick he was able to make a large-diameter hollow LIGHT PIPE [trademark] which avoids even the small losses in the Lucite itself! Using this trick he is able to "pipe" large amounts of light from single (efficient) light sources [including rooftop solar collectors] into other areas [like the interiors of office buildings] using strictly passive components that do not wear out. He founded a company called TIR - see if you can guess what the acronym stands for!

Footnotes

. . . slowly.^14.18

Boy, is this ever Aristotelian!

. . . LAW:^14.19

SNELL'S LAW is normally expressed in terms of the INDEX OF REFRACTION $n$ in each medium:

$$n \; \sin(\theta) \; = \; n' \; \sin(\theta') ,$$

where (we now know) the INDEX OF REFRACTION is the ratio of the speed of light in vacuum to the speed of light in the medium:

$$n \; \equiv \; {c_{_0} \over c} .$$

The reason for inventing such a semicircular definition was that when Willebrord Snell discovered this empirical relationship in 1621 he had no idea what $n$ was, only that every medium had its own special value of $n$. (This is typical of anything that gets the name "index.") I see no pedagogical reason to even define the dumb thing.

. . . continuous^14.20

A "crest" doesn't turn into a "trough" just because the propagation velocity changes!