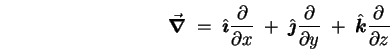- A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE
The utility of thinking of ![]() as a "ray"
becomes even more obvious when we get away from plane waves
and start thinking of waves with curved wavefronts.
The simplest such wave is the type that is emitted when
a pebble is tossed into a still pool - an example of
the "point source" that radiates waves isotropically
in all directions. The wavefronts are then circles
in two dimensions (the surface of the pool) or spheres
in three dimensions (as for sound waves) separated by one
wavelength
as a "ray"
becomes even more obvious when we get away from plane waves
and start thinking of waves with curved wavefronts.
The simplest such wave is the type that is emitted when
a pebble is tossed into a still pool - an example of
the "point source" that radiates waves isotropically
in all directions. The wavefronts are then circles
in two dimensions (the surface of the pool) or spheres
in three dimensions (as for sound waves) separated by one
wavelength ![]() and heading outward
from the source at the propagation velocity
and heading outward
from the source at the propagation velocity ![]() .
In this case the "rays"
.
In this case the "rays" ![]() point along
the radius vector
point along
the radius vector ![]() from the source
at any position and we can once again write down a rather simple
formula for the "wave function"
(displacement
from the source
at any position and we can once again write down a rather simple
formula for the "wave function"
(displacement ![]() as a function of position)
that depends only on the time
as a function of position)
that depends only on the time ![]() and the scalar
distance
and the scalar
distance ![]() from the source.
from the source.
A plausible first guess would be just
![]() ,
but this cannot be right! Why not?
Because it violates energy conservation.
The energy density stored in a wave is proportional to
the square of its amplitude; in the trial solution above,
the amplitude of the outgoing spherical wavefront is
constant as a function or
,
but this cannot be right! Why not?
Because it violates energy conservation.
The energy density stored in a wave is proportional to
the square of its amplitude; in the trial solution above,
the amplitude of the outgoing spherical wavefront is
constant as a function or ![]() , but the area
of that wavefront increases as
, but the area
of that wavefront increases as ![]() .
Thus the energy in the wavefront increases as
.
Thus the energy in the wavefront increases as ![]() ?
I think not. We can get rid of this effect by just dividing
the amplitude by
?
I think not. We can get rid of this effect by just dividing
the amplitude by ![]() (which divides the energy density by
(which divides the energy density by ![]() ).
Thus a trial solution is
).
Thus a trial solution is
We won't use this equation for anything right now, but it is interesting to know that it does accurately describe an outgoing14.12spherical wave.
The perceptive reader will have noticed by now that Eq. (38)
is not a solution to the WAVE EQUATION as represented
in one dimension by Eq. (10).
That is hardly surprising, since the spherical wave solution is
an intrinsically 3-dimensional beast; what happened to ![]() and
and ![]() ?
The correct vector form of the WAVE EQUATION is
?
The correct vector form of the WAVE EQUATION is