 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE Some of the more peculiar properties of temperature can be illustrated by a simple example:
Certain particles such as electrons have "spin
![]() "
which (it turns out) prevents their spins from having
any orientation in a magnetic field
"
which (it turns out) prevents their spins from having
any orientation in a magnetic field ![]() other than parallel to the field ("spin up")
or antiparallel to it ("spin down").
Because each electron has a magnetic moment
other than parallel to the field ("spin up")
or antiparallel to it ("spin down").
Because each electron has a magnetic moment ![]() (sort of like a tiny compass needle)
lined up along its spin direction,
there is an energy
(sort of like a tiny compass needle)
lined up along its spin direction,
there is an energy
![]() associated with its orientation in the field.15.21
For a "spin up" electron
the energy is
associated with its orientation in the field.15.21
For a "spin up" electron
the energy is
![]() and for a "spin down" electron
the energy is
and for a "spin down" electron
the energy is
![]() .
.
Consider a system consisting of N electrons
in a magnetic field and neglect all other interactions,
so that the total energy U of the system is given by
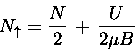 |
(15.15) |
This system is another example of the binomial distribution
whose multiplicity function was given by Eq. (1),
with
![]() in place of n.
This can be easily converted to
in place of n.
This can be easily converted to ![]() .
The entropy
.
The entropy ![]() is then just
the logarithm of
is then just
the logarithm of ![]() ,
as usual.
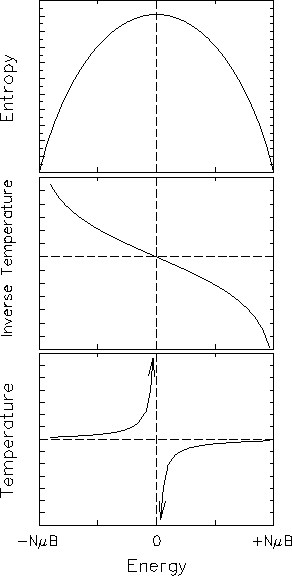
The result is plotted in the top frame of Fig. 15.2
as a function of energy. Note that the entropy has a
maximum value for equal numbers of spins
up and down - i.e. for zero energy.
There must be some such peak in
,
as usual.
The result is plotted in the top frame of Fig. 15.2
as a function of energy. Note that the entropy has a
maximum value for equal numbers of spins
up and down - i.e. for zero energy.
There must be some such peak in ![]() whenever
the energy is bounded above - i.e.
whenever there is a maximum possible energy
that can be stored in the system. Such situations
do occur [this is a "real" example!] but they are rare;
usually the system will hold as much energy as you want.
whenever
the energy is bounded above - i.e.
whenever there is a maximum possible energy
that can be stored in the system. Such situations
do occur [this is a "real" example!] but they are rare;
usually the system will hold as much energy as you want.
 |