BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Imaginary Exponents
Up: Simple Harmonic Motion
Previous: Simple Harmonic Motion
Another mecahnical example will serve to establish the paradigm
of SIMPLE HARMONIC MOTION (SHM) as a solution to a particular
type of equation of motion.13.4
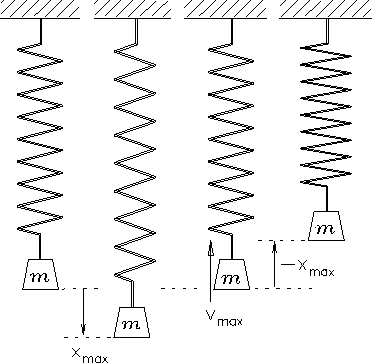
Figure:
Successive "snapshots" of a mass
bouncing up and down on a spring.
 |
As discussed in a previous chapter,
the spring embodies one of Physics' premiere paradigms,
the linear restoring force. That is, a force which disappears
when the system in question is in its "equilibrium position"
x0 [which we will define as the x = 0 position
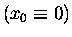 to make the calculations easier]
but increases as x moves away from equilibrium,
in such a way that the magnitude of the force F
is proportional to the displacement from equilibrium
[F is linear in x] and the direction
of F is such as to try to restore x to
the original position. The constant of proportionality
is called the spring constant, always written k.
Thus F = - k x and the resultant equation of motion is
to make the calculations easier]
but increases as x moves away from equilibrium,
in such a way that the magnitude of the force F
is proportional to the displacement from equilibrium
[F is linear in x] and the direction
of F is such as to try to restore x to
the original position. The constant of proportionality
is called the spring constant, always written k.
Thus F = - k x and the resultant equation of motion is
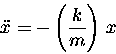 |
(13.10) |
Note that the mass plays a rôle just as essential
as the linear restoring force in this paradigm.
If 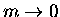 in this equation, then the acceleration
becomes infinite and in principle the spring would just
return instantaneously to its equilibrium length and stay there!
in this equation, then the acceleration
becomes infinite and in principle the spring would just
return instantaneously to its equilibrium length and stay there!
In the leftmost frame of Fig. 13.4
the mass m is at rest and the spring
is in its equilibrium position (i.e. neither stretched nor compressed)
defined as x=0.
In the second frame, the spring has been gradually pulled down
a distance
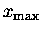 and the mass is once again at rest.
Then the mass is released and accelerates upward under the
influence of the spring until it reaches the equilibrium position
again [third frame]. This time, however, it is moving at its
maximum velocity
and the mass is once again at rest.
Then the mass is released and accelerates upward under the
influence of the spring until it reaches the equilibrium position
again [third frame]. This time, however, it is moving at its
maximum velocity
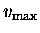 as it crosses the centre position;
as soon as it goes higher, it compresses the spring and
begins to be decelerated by a linear restoring force in the
opposite direction. Eventually, when
as it crosses the centre position;
as soon as it goes higher, it compresses the spring and
begins to be decelerated by a linear restoring force in the
opposite direction. Eventually, when
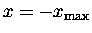 ,
all the kinetic energy has been been stored back up in the compression
of the spring and the mass is once again instantaneously at rest
[fourth frame]. It immediately starts moving downward again at
maximum acceleration and heads back toward its starting point.
In the absence of friction, this cycle will repeat forever.
,
all the kinetic energy has been been stored back up in the compression
of the spring and the mass is once again instantaneously at rest
[fourth frame]. It immediately starts moving downward again at
maximum acceleration and heads back toward its starting point.
In the absence of friction, this cycle will repeat forever.
I now want to call your attention to the acute similarity
between the above differential equation and the one we solved
for exponential decay:
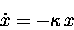 |
(13.11) |
and, by extension,
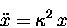 |
(13.12) |
the solution to which equation of motion
(i.e. the function which "satisfies" the differential equation)
was
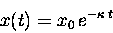 |
(13.13) |
Now, if only we could equate 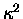 with - k/m,
these equations of motion (and therefore their solutions)
would be exactly the same! The problem is, of course,
that both k and m are intrinsically positive constants,
so it is tough to find a real constant
with - k/m,
these equations of motion (and therefore their solutions)
would be exactly the same! The problem is, of course,
that both k and m are intrinsically positive constants,
so it is tough to find a real constant 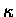 which
gives a negative number when squared.
which
gives a negative number when squared.


Next: Imaginary Exponents
Up: Simple Harmonic Motion
Previous: Simple Harmonic Motion
Jess H. Brewer -
Last modified: Sun Nov 15 13:36:04 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE 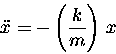
![]() and the mass is once again at rest.
Then the mass is released and accelerates upward under the
influence of the spring until it reaches the equilibrium position
again [third frame]. This time, however, it is moving at its
maximum velocity
and the mass is once again at rest.
Then the mass is released and accelerates upward under the
influence of the spring until it reaches the equilibrium position
again [third frame]. This time, however, it is moving at its
maximum velocity
![]() as it crosses the centre position;
as soon as it goes higher, it compresses the spring and
begins to be decelerated by a linear restoring force in the
opposite direction. Eventually, when
as it crosses the centre position;
as soon as it goes higher, it compresses the spring and
begins to be decelerated by a linear restoring force in the
opposite direction. Eventually, when
![]() ,
all the kinetic energy has been been stored back up in the compression
of the spring and the mass is once again instantaneously at rest
[fourth frame]. It immediately starts moving downward again at
maximum acceleration and heads back toward its starting point.
In the absence of friction, this cycle will repeat forever.
,
all the kinetic energy has been been stored back up in the compression
of the spring and the mass is once again instantaneously at rest
[fourth frame]. It immediately starts moving downward again at
maximum acceleration and heads back toward its starting point.
In the absence of friction, this cycle will repeat forever.