Rod of Current

As an exercise in the "brute force" integration of the LAW OF BIOT & SAVART (unavoidable in most cases), here is one way to find the magnetic field due to a current I flowing in a skinny rod of finite length L. (Of course the current cannot just start at one end and stop at the other, but the field due to the rest of the circuit can be added in separately.)

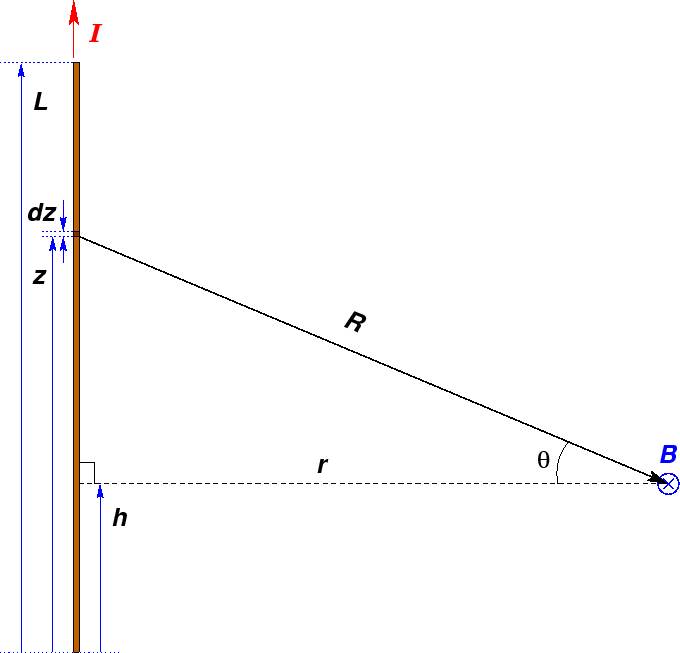
According to the LAW OF BIOT & SAVART, the current element $I \, dz$ shown in the Figure contributes

$$d\Vec{B} = {\mu_0 \over 4 \pi} \, I \, dz \, \left( \kH \times \Hat{R} \over R^2 \right)$$ (1)

to the magnetic field $\Vec{B}$ at the "test point" shown, where

$$R = \sqrt{ r^2 + (z-h)^2 }$$ (2)

is the distance from the current element to the test point, r is its perpendicular distance from the rod and h is its distance up from the bottom end of the rod, measured parallel to the rod. The "test point" is characterized completely by r and h.

We choose to look at the rod and the point in their common plane. Thus the direction of $\Vec{B}$ can be seen by inspection to be into the page. In fact $\Vec{B}$ circulates around the rod in circular loops according to the Right Hand Rule.

To integrate equation (1) we need to convert all variables to match the differential (over which we integrate).

We could use Eq. (2) to express R in terms of z (where r and h are constants) and use

$$\cos \theta = {r \over R}$$ (3)

$$\sin \theta = {(z-h) \over R}$$ (4)

but this would leave us with integrals that cannot be solved by inspection.

If we want to solve this problem without reference to external aids (like tables of integrals), it is better to convert into angles and trigonometric functions as follows:

Equation (3) can be rewritten

$${1 \over R^2} = {\cos^2 \theta \over r^2}$$ (5)

and since

$$z - h = r \tan \theta \; ,$$ (6)

giving

$$dz = r \sec^2 \theta \; d\theta = {r \, d\theta \over \cos^2 \theta} \; ,$$ (7)

we can write Eq. (1) as

 

$${\mu_0 I \over 4 \pi} \, \cos \theta \, \left(\cos^2 \theta \over r^2 \right) \left(r \, d\theta \over \cos^2 \theta \right) \cr$$ dB = (8)

or

$$dB = {\mu_0 I \over 4 \pi r} \, du$$ (9)

where $u \equiv \sin \theta$.

Integrating this differential is trivial; we are left with just the difference between u at the limits of integration (the top and bottom of the rod):

$$B = {\mu_0 I \over 4 \pi r} \, \left[ { (L-h) \over \sqrt{r^2 + (L-h)^2} } + { h \over \sqrt{r^2 + h^2} } \right]$$

(10)

(note that u is negative at the bottom).

This equation expresses a completely general solution to this problem.

Let's check to see what this gives for the field directly out from the midpoint of the rod - i.e. for h = L/2:

 

$${\mu_0 I \over 4 \pi r} \, \left[ { L/2 \over \sqrt{r^2 + L^2/4} } + { L/2 \over \sqrt{r^2 + L^2/4} } \right] \cr$$ B = (11)

Let's also check to see what we get (at the midpoint) very far from the rod ($r \gg L$):

$$B \goestoas{r \to \infty} {\mu_0 I \over 4 \pi r} \, { L \over r } = {\mu_0 I L \over 4 \pi r^2}$$ (12)

and very close to the rod ($r \ll L$):

$$B \goestoas{r \to 0} {\mu_0 I \over 4 \pi r} \, { L \over L/2 } = {\mu_0 I \over 2 \pi r} \, .$$ (13)

The last result can be used as the field due to an infinitely long current-carrying wire. But there is a much easier way to obtain it . . . .

Note that the general formula (10) (and the right-hand rule to determine directions) can be used to find the net $\Vec{B}$ from a circuit composed of any arrangement of straight wire segments carrying a current I, by the principle of superposition. Note also, however, that the result is a vector sum.