BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Bohr's Energy Levels
Up: Fudging The Bohr Atom
Previous: Fudging The Bohr Atom
We can play more games with Bohr's hydrogen atom if we like,
using just Eq. (8) to relate rn and pn.
Suppose we ask, "What is keeping the electron in its orbit?"
The answer is, of course, "The Coulomb force of attraction
between the positive nucleus and the negative electron!"
This centripetal force has the value (in SI units)
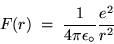 |
(24.10) |
where
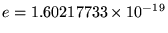 C
is the magnitude of the charge on either an electron
(-e) or a proton (+e) and the ugly mess out front is the legacy
of SI units - a constant stuck in to make it come out right.
The corresponding electrostatic potential energy is
C
is the magnitude of the charge on either an electron
(-e) or a proton (+e) and the ugly mess out front is the legacy
of SI units - a constant stuck in to make it come out right.
The corresponding electrostatic potential energy is
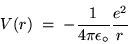 |
(24.11) |
(relative to 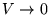 at
at
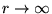 ).
We'll need that momentarily.
).
We'll need that momentarily.
A simple application of NEWTON'S SECOND LAW gives
where m is the mass of the electron.
Cancelling one r and rearranging gives
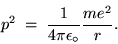 |
(24.12) |
Substituting Eq. (8) into Eq. (12) gives
or (after some shuffling)
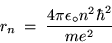 |
(24.13) |
for the radius of the
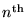 Bohr orbit of the H atom.
The lowest orbit (n = 1) has a special name and symbol:
the BOHR RADIUS,
Bohr orbit of the H atom.
The lowest orbit (n = 1) has a special name and symbol:
the BOHR RADIUS,
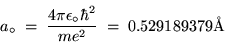 |
(24.14) |
where 1 Å = 10-10 m.


Next: Bohr's Energy Levels
Up: Fudging The Bohr Atom
Previous: Fudging The Bohr Atom
Jess H. Brewer -
Last modified: Wed Nov 18 17:29:17 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE