BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Impulse and Momentum
Up: Some Math Tricks
Previous: Differentials
Suppose we have a function g(x) which we know is the derivative
[with respect to x] of some other function f(x), but
we don't know which - i.e. we know g(x) explicitly
but we don't know [yet] what f(x) it is the derivative of.
We may then ask the question, "What is the function f(x)
whose derivative [with respect to x] is g(x)?"
Another way of putting this would be to ask,
"What is the antiderivative of g(x)?"11.1
Another name for the antiderivative is the integral,
which is in fact the "official" version, but I like the former better
because the name suggests how we go about "solving"
one.11.2
For a handy example consider
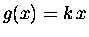 .
Then the antiderivative [integral] of g(x) with respect to x
is
.
Then the antiderivative [integral] of g(x) with respect to x
is
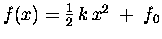 [where f0 is some constant] because the derivative
[with respect to x] of x2 is 2x and the derivative of
any constant is zero. Since any combination of constants
is also a constant, it is equally valid to make the
arbitrary constant term of the same form as the part which
actually varies with x, viz.
[where f0 is some constant] because the derivative
[with respect to x] of x2 is 2x and the derivative of
any constant is zero. Since any combination of constants
is also a constant, it is equally valid to make the
arbitrary constant term of the same form as the part which
actually varies with x, viz.
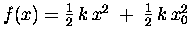 .
Thus f0 is the same thing as
.
Thus f0 is the same thing as
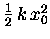 and it is a matter of taste which you want to use.
and it is a matter of taste which you want to use.
Naturally we have a shorthand way of writing this.
The differential equation
can be turned into the integral equation
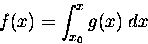 |
(11.2) |
which reads,
"f(x) is the integral of g(x) with respect to x from x0 to x."
We have used the rule that the integral of the differential
of f [or any other quantity] is just the quantity itself,11.3
in this case f:
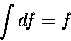 |
(11.3) |
Our example then reads
where we have used the feature that any constant (like k)
can be brought "outside the integral" - i.e. to the left
of the integral sign
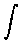 .
.
Now let's use these new tools to transform Newton's SECOND LAW
into something more comfortable.


Next: Impulse and Momentum
Up: Some Math Tricks
Previous: Differentials
Jess H. Brewer -
Last modified: Sat Nov 14 12:38:58 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE ![]() .
Then the antiderivative [integral] of g(x) with respect to x
is
.
Then the antiderivative [integral] of g(x) with respect to x
is
![]() [where f0 is some constant] because the derivative
[with respect to x] of x2 is 2x and the derivative of
any constant is zero. Since any combination of constants
is also a constant, it is equally valid to make the
arbitrary constant term of the same form as the part which
actually varies with x, viz.
[where f0 is some constant] because the derivative
[with respect to x] of x2 is 2x and the derivative of
any constant is zero. Since any combination of constants
is also a constant, it is equally valid to make the
arbitrary constant term of the same form as the part which
actually varies with x, viz.
![]() .
Thus f0 is the same thing as
.
Thus f0 is the same thing as
![]() and it is a matter of taste which you want to use.
and it is a matter of taste which you want to use.