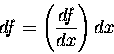BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Antiderivatives
Up: Some Math Tricks
Previous: Some Math Tricks
We have learned that the symbols df and dx
represent the coupled changes in f(x) and x,
in the limit where the change in x
(and consequently also the change in f)
become infinitesimally small.
We call these symbols the differentials of f and x
and distinguish them from 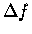 and
and 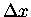 only in this sense:
only in this sense: 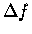 and
and 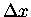 can be any size,
but df and dx are always infinitesimal - i.e.
small enough so that we can treat f(x) as a straight line
over an interval only dx wide.
can be any size,
but df and dx are always infinitesimal - i.e.
small enough so that we can treat f(x) as a straight line
over an interval only dx wide.
This does not change the interpretation of the representation
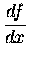 for the derivative of f(x) with respect to x,
but it allows us to think of these differentials
df and dx as "normal" algebraic symbols that can be
manipulated in the usual fashion. For instance, we can write
for the derivative of f(x) with respect to x,
but it allows us to think of these differentials
df and dx as "normal" algebraic symbols that can be
manipulated in the usual fashion. For instance, we can write
which looks rather trivial in this form.
However, suppose we give the derivative its own name:
Then the previous equation reads
which can now be read as an expression of the
relationship between the two differentials
df and dx. Hold that thought.
As an example, consider our familiar kinematical quantities
If we treat the differentials as simple algebraic symbols,
we can invert the latter definition and write
(Don't worry too much about what this "means" for now.)
Then we can multiply the left side of the definition of a
by 1/v and multiply the right side by dt/dx and get an
equally valid equation:
or, multiplying both sides by 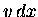 ,
,
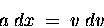 |
(11.1) |
which is a good example of a mathematical identity,
in this case involving the differentials of distance and velocity.
Hold that thought.


Next: Antiderivatives
Up: Some Math Tricks
Previous: Some Math Tricks
Jess H. Brewer -
Last modified: Sat Nov 14 12:37:41 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE ![]() for the derivative of f(x) with respect to x,
but it allows us to think of these differentials
df and dx as "normal" algebraic symbols that can be
manipulated in the usual fashion. For instance, we can write
for the derivative of f(x) with respect to x,
but it allows us to think of these differentials
df and dx as "normal" algebraic symbols that can be
manipulated in the usual fashion. For instance, we can write