 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE
If we form the scalar ("dot") product
of ![]() with a vector function
with a vector function
![]() we get a scalar result called the DIVERGENCE of
we get a scalar result called the DIVERGENCE of ![]() :
:
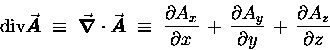
"What leaves a region is no longer in it."
For example, consider the divergence of the CURRENT DENSITY
![]() ,
which describes the FLUX of
a CONSERVED QUANTITY such as electric charge Q.
(Mass, as in the current of a river, would do just as well.)
,
which describes the FLUX of
a CONSERVED QUANTITY such as electric charge Q.
(Mass, as in the current of a river, would do just as well.)
It may not depend on z at all, of course. In this case, the amount of Q coming into the cube through the bottom surface (per unit time) will be the same as the amount of Q going out through the top surface and there will be no net gain or loss of Q in the volume - at least not due to Jz.
If Jz is bigger at the top, however, there will
be a net loss of Q within the volume dV
due to the "divergence" of Jz.
Let's see how much: the difference between
Jz(z) at the bottom and Jz(z+dz) at the top
is, by definition,
![]() .
The flux is over the same area at top and bottom,
namely
.
The flux is over the same area at top and bottom,
namely ![]() ,
so the total rate of loss
of Q due to the z-dependence of Jz is given by
,
so the total rate of loss
of Q due to the z-dependence of Jz is given by
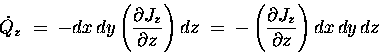
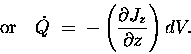
A perfectly analogous argument holds for the x-dependence
if Jx and the y-dependence of Jy, giving a total
rate of change of Q
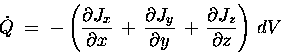
The total amount of Q in our volume element dV
at a given instant is just
![]() ,
of course,
so the rate of change of the enclosed Q is just
,
of course,
so the rate of change of the enclosed Q is just
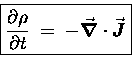
This equation tells us that the "Q sourciness"
of each point in space is given by the degree to which
flux "lines" of ![]() tend to radiate away
from that point more than they converge toward
that point - namely, the DIVERGENCE of
tend to radiate away
from that point more than they converge toward
that point - namely, the DIVERGENCE of ![]() at the point in question. This esoteric-looking mathematical
expression is, remember, just a formal way of expressing
our original dumb tautology!
at the point in question. This esoteric-looking mathematical
expression is, remember, just a formal way of expressing
our original dumb tautology!