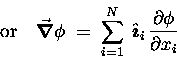- A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE
It is instructive to work up to this "one dimension at a time."
For simplicity we will stick to using ![]() as the symbol
for the function of which we are taking derivatives.
as the symbol
for the function of which we are taking derivatives.
The GRADIENT in One Dimension
Let the dimension be x. Then we have no "extra" variables
to hold constant and the gradient of ![]() is nothing
but
is nothing
but
![]() .
We can illustrate the "meaning"
of
.
We can illustrate the "meaning"
of
![]() by an example: let
by an example: let ![]() be the mass of an
object times the acceleration of gravity times the height h of
a hill at horizontal position x. That is,
be the mass of an
object times the acceleration of gravity times the height h of
a hill at horizontal position x. That is, ![]() is the
gravitational potential energy of the object when it is
at horizontal position x. Then
is the
gravitational potential energy of the object when it is
at horizontal position x. Then
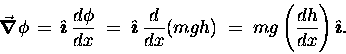
The GRADIENT in Two Dimensions
In the previous example we disregarded the fact that most hills
extend in two horizontal directions, say x = East
and y = North. [If we stick to small distances we won't notice
the curvature of the Earth's surface.]
In this case there are two components to the slope:
the Eastward slope
![]() and the Northward slope
and the Northward slope
![]() .
The former is a measure of how steep the hill will seem
if you head due East and the latter is a measure of how steep
it will seem if you head due North. If you put these together
to form a vector "steepness" (gradient)
.
The former is a measure of how steep the hill will seem
if you head due East and the latter is a measure of how steep
it will seem if you head due North. If you put these together
to form a vector "steepness" (gradient)
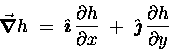
The GRADIENT in Three Dimensions
If the potential ![]() is a function of 3 variables,
is a function of 3 variables,
![]() [such as the three spatial coordinates
x, y and z - in which case we can write it a little
more compactly as
[such as the three spatial coordinates
x, y and z - in which case we can write it a little
more compactly as
![]() where
where
![]() ,
the vector distance
from the origin of our coordinate system to the point in space
where
,
the vector distance
from the origin of our coordinate system to the point in space
where ![]() is being evaluated], then
it is a little more difficult to make up a "hill" analogy
-- try imagining a topographical map in the form of
a 3-dimensional hologram where instead of lines of
constant altitude the "equipotentials" are
surfaces of constant
is being evaluated], then
it is a little more difficult to make up a "hill" analogy
-- try imagining a topographical map in the form of
a 3-dimensional hologram where instead of lines of
constant altitude the "equipotentials" are
surfaces of constant ![]() .
(This is just what
Physicists do picture!) Fortunately the math
extends easily to 3 dimensions (or any larger number,
if that has any meaning in the context we choose).
.
(This is just what
Physicists do picture!) Fortunately the math
extends easily to 3 dimensions (or any larger number,
if that has any meaning in the context we choose).
In general, any time there is a potential energy
function
![]() we can immediately write down the
force
we can immediately write down the
force ![]() associated with it as
associated with it as
The GRADIENT in N Dimensions
Although we won't be needing to go beyond 3 dimensions very often
in Physics, you might want to borrow this metaphor for application
in other realms of human endeavour where there are more than 3
variables of which your scalar field is a function.
You could have ![]() be a measure of happiness,
for instance [though it is hard to take reliable measurements
on such a subjective quantity]; then
be a measure of happiness,
for instance [though it is hard to take reliable measurements
on such a subjective quantity]; then ![]() might be a function
of lots of factors, such as x1 = freedom from violence,
x2 = freedom from hunger, x3 = freedom from poverty,
x4 = freedom from oppression, and so on.3
Note that with an arbitrary number of variables we get away from
thinking up different names for each one and just call the
might be a function
of lots of factors, such as x1 = freedom from violence,
x2 = freedom from hunger, x3 = freedom from poverty,
x4 = freedom from oppression, and so on.3
Note that with an arbitrary number of variables we get away from
thinking up different names for each one and just call the
![]() variable "xi."
variable "xi."
Then we can define the GRADIENT in N dimensions as