BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Gravity
Up: Gauss' Law
Previous: Gauss' Law
For example, consider a hypothetical "spherically symmetric"
sprinkler head (perhaps meant to
uniformly irrigate the inside surface
of a hollow spherical space colony): located at the
centre of the sphere, it "emits" (squirts out)
dQ/dt gallons per second
of water in all directions equally,
which is what we mean by "spherically symmetric" or
"isotropic."18.1
Here Q is the "amount of stuff" -
in this case measured in gallons.
Obviously (beware of that word, but it's OK here),
since water is conserved
the total flow of water is conserved:
once a "steady-state" (equilibrated) flow has been
established, the rate at which water
is deposited on the walls of the sphere is the same as the rate
at which water is emitted from the sprinkler head at the
centre. That is, if we add up (integrate)
the "flux" 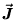 of
water per second per square meter of surface area at the sphere
wall over the whole spherical surface, we must get dQ/dt.
Mathematically, this is written
of
water per second per square meter of surface area at the sphere
wall over the whole spherical surface, we must get dQ/dt.
Mathematically, this is written
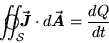 |
(18.1) |
where the
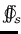 stands for an integral (sum of elements)
over a closed surface
stands for an integral (sum of elements)
over a closed surface 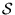 .
[This part is crucial,
inasmuch as an open surface (like a hemisphere)
does not account for all the flux and cannot be used with
GAUSS' LAW].
Now, we must pay a little attention to the vector
notation: the "flux"
.
[This part is crucial,
inasmuch as an open surface (like a hemisphere)
does not account for all the flux and cannot be used with
GAUSS' LAW].
Now, we must pay a little attention to the vector
notation: the "flux" 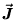 always has a direction,
like the flux (current) of water flowing in a river
or in this case the flux of water droplets
passing through space.
always has a direction,
like the flux (current) of water flowing in a river
or in this case the flux of water droplets
passing through space.
Figure:
An isotropic source.
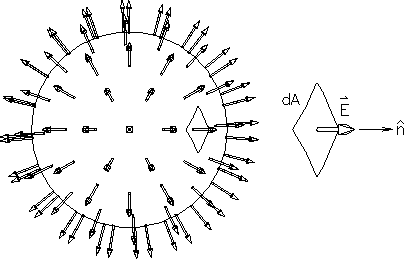 |
Each droplet has a
(vector) velocity, and the velocity
and the density of droplets combine to form the "flux"
as described above. Not so trivial is the idea of a
vector area element 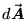 ,
but the sense of this is
clear if we think of what happens to the scalar flux
(in gallons/sec) through a hoop of wire of area
,
but the sense of this is
clear if we think of what happens to the scalar flux
(in gallons/sec) through a hoop of wire of area 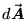 when we place it in a river: if the direction of the
flow of the river is perpendicular ("normal") to the plane
of the hoop, we get the maximum possible flux, namely
the vector flux magnitude (the flow rate of the river)
times the area of the hoop; if we reorient the hoop
so that its area intercepts no flow (i.e. if the
direction
when we place it in a river: if the direction of the
flow of the river is perpendicular ("normal") to the plane
of the hoop, we get the maximum possible flux, namely
the vector flux magnitude (the flow rate of the river)
times the area of the hoop; if we reorient the hoop
so that its area intercepts no flow (i.e. if the
direction 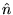 "normal" to the plane of the hoop is
perpendicular to the direction of flow of the river)
then we get zero flux through the hoop. In general,
the scalar rate of flow (here measured in gallons/sec)
through a "surface element"
"normal" to the plane of the hoop is
perpendicular to the direction of flow of the river)
then we get zero flux through the hoop. In general,
the scalar rate of flow (here measured in gallons/sec)
through a "surface element" 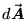 whose "normal" direction
whose "normal" direction
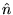 is given by
is given by
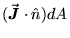 or just
or just
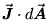 where we
have now defined the vector surface element
where we
have now defined the vector surface element
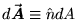 .
This is pictured in Fig. 18.1 above.
.
This is pictured in Fig. 18.1 above.
Returning now to our sprinkler-head example,
we have a Law [Eq. (1)]
which is a mathematical (and therefore
quantitative) statement of the colloquial form,
which in principle allows us to calculate something.
However, it is still of only academic interest in general. Why?
Because the integral described in Eq. (1) is so general
that it may well be hopelessly difficult to solve,
unless (!) there is something about the symmetry
of the particular case under consideration that makes
it easy, or even "trivial." Fortunately (though hardly
by accident) in this case there is - namely, the
isotropic nature of the sprinkler head's
emission, plus the spherically symmetric
(in fact, spherical) shape of the surface designated by
" " in Eq. (1).
These two features ensure that
" in Eq. (1).
These two features ensure that
- 1.
- the magnitude
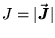 of the flux
is the same everywhere on the surface
of the flux
is the same everywhere on the surface 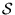 ;
and
;
and
- 2.
- the direction of
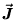 is normal to
the surface everywhere it hits on
is normal to
the surface everywhere it hits on 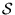 .
.
In this case,
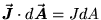 and J is now a constant which can be taken
outside the integral sign, leaving
and J is now a constant which can be taken
outside the integral sign, leaving
where 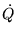 is just a compact notation for dQ/dt.
But
is just a compact notation for dQ/dt.
But
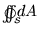 is just the area of the sphere,
is just the area of the sphere, 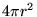 ,
where r is the radius of the sphere,
so (1) becomes
,
where r is the radius of the sphere,
so (1) becomes
or
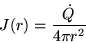 |
(18.2) |
which states the general conclusion for any
spherically symmetric emission of a conserved quantity, namely
The flux from an isotropic source
points away from the centre and falls off proportional to
the inverse square of the distance from the source.
This holds in an amazing variety of situations.
For instance, consider the "electric field lines"
from a spherically symmetric electric charge distribution
as measured at some point a distance r away from the centre.
We visualize these electric field "lines" as streams of
some mysterious "stuff" being "squirted out" by
positive charges (or "sucked in" by negative charges).
The idea of an electric field line is of course
a pure construct; no one has ever seen
or ever will see a "line" of
the electric field 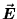 ,
but if we think of the strength
of
,
but if we think of the strength
of 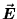 as the "number of field lines per unit area
perpendicular to
as the "number of field lines per unit area
perpendicular to 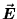 " and treat these "lines of force" as if
they were conserved in the same way as streams of
water, we get a useful graphical picture as well as a
model which, when translated into mathematics, gives
correct answers. As suspicious as this may sound, it is really
all one can ask of a physical model of something we cannot see.
This is the sense of all sketches showing electric field lines.
For every little bit ("element") of charge dq
on one side of the symmetric distribution there is an
equal charge element exactly opposite (relative to the
radius vector joining the centre to the point at which we are
evaluating
" and treat these "lines of force" as if
they were conserved in the same way as streams of
water, we get a useful graphical picture as well as a
model which, when translated into mathematics, gives
correct answers. As suspicious as this may sound, it is really
all one can ask of a physical model of something we cannot see.
This is the sense of all sketches showing electric field lines.
For every little bit ("element") of charge dq
on one side of the symmetric distribution there is an
equal charge element exactly opposite (relative to the
radius vector joining the centre to the point at which we are
evaluating 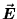 ); the "transverse" contributions of such
charge elements to
); the "transverse" contributions of such
charge elements to 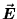 all cancel out, and so the only
possible direction for
all cancel out, and so the only
possible direction for 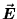 to point is along the
radius vector - i.e. as described above.
An even simpler argument is that
there is no way to pick a preferred direction
(other than the radial direction) if the charge distribution
truly has spherical symmetry.
This "symmetry argument" is implied in Fig. 18.1.
to point is along the
radius vector - i.e. as described above.
An even simpler argument is that
there is no way to pick a preferred direction
(other than the radial direction) if the charge distribution
truly has spherical symmetry.
This "symmetry argument" is implied in Fig. 18.1.
Now we must change our notation slightly from the
general description of Eqs. (1)
and (2) to the specific
example of electric charge and field.
Inasmuch as one's choice of a system of units
in electromagnetism is rather flexible, and since
each choice introduces a different set of constants
of proportionality with odd units of their own, I will
merely state that "J turns into E,
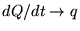 now stands for electric charge,
and there is a
now stands for electric charge,
and there is a
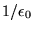 in front of the
in front of the
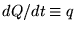 on the right-hand side of Eq. (1)" to give us the
electrostatics version of (1):
on the right-hand side of Eq. (1)" to give us the
electrostatics version of (1):
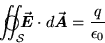 |
(18.3) |
which, when applied to the isotropic charge
distribution, gives the result
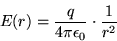 |
(18.4) |
The implication of Eq. (3) is then that, since the
spherical shell contains the same amount of charge
for all radii r > R, where R is the physical radius
of the charge distribution itself, it cannot matter how
the charge is distributed (as long as it is
spherically symmetric); to the distant observer,
the 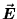 field it produces will always look just like
the
field it produces will always look just like
the 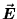 field due to a point charge q at the
centre; i.e. Eq. (4).
field due to a point charge q at the
centre; i.e. Eq. (4).


Next: Gravity
Up: Gauss' Law
Previous: Gauss' Law
Jess H. Brewer -
Last modified: Mon Nov 16 17:26:23 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE ![]() of
water per second per square meter of surface area at the sphere
wall over the whole spherical surface, we must get dQ/dt.
Mathematically, this is written
of
water per second per square meter of surface area at the sphere
wall over the whole spherical surface, we must get dQ/dt.
Mathematically, this is written
![]() " in Eq. (1).
These two features ensure that
" in Eq. (1).
These two features ensure that
![]() now stands for electric charge,
and there is a
now stands for electric charge,
and there is a
![]() in front of the
in front of the
![]() on the right-hand side of Eq. (1)" to give us the
electrostatics version of (1):
on the right-hand side of Eq. (1)" to give us the
electrostatics version of (1):