BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Up: The Free Body Diagram
Previous: The Free Body Diagram
To illustrate the use of the FBD in nontrivial mechanics problems
we can imagine another series of measurements9
with a simple device known as Atwood's Machine.
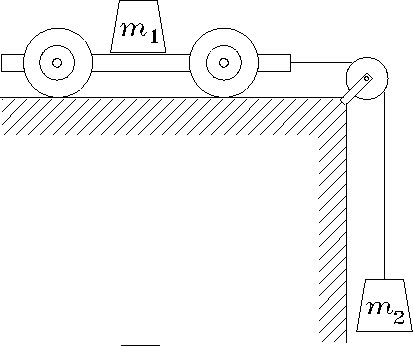
The apparatus is pictured in Fig. 2.
Figure:
Atwood's Machine - one object labelled m1
is glued to a massless cart with massless wheels that roll
without friction on a perfectly horizontal surface.
The cart is attached to a massless, unstretchable string
that runs over yet another massless, frictionless pulley
and is attached at the other end to a second object labelled m2
that is pulled downward by the force of gravity.
[You can see that a real experiment might involve a few corrections!]
At the right are pictured the two separate FBD's for m1 and m2,
showing all the external forces acting on each.
Here W1 is the weight of m1 and N is the
normal force exerted on m1 by the horizontal surface
(through the cart) to keep it from falling.
Since it does not fall, N must exactly balance W1.
The only unbalanced force on m1 is
the tension T in the string,
which accelerates it to the right.
The tension in a string is the same everywhere,
so the same T pulls up on m2,
partly counteracting its weight W2.
 |
It is easy to see that the two vertical forces (W1 and N)
acting on m1 must cancel. The rest is less trivial.
The weight of m2 is given by
 ;
thus
for m1 and m2, respectively, we have the
"equations of motion"
;
thus
for m1 and m2, respectively, we have the
"equations of motion"
and
But we have here three unknowns (a1, a2 and T)
and only two equations. The rules of linear algebra
say that we need at least as many equations as unknowns
to find a solution! Our salvation lies in recognition
of the constraints of the system:
Because the string does not stretch or go limp,
both masses are constrained to move exactly
the same distance (though in different directions)
and therefore both experience the same magnitude
of acceleration a. Thus our third equation is
a1 = a2 = a and we can equate the right sides
of the two previous equations to get
which we multiply through by
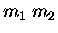 to get
to get
Plugging this back into our first equation gives

A quicker, simpler, more intuitive
(and thus riskier)
way of seeing this is to picture the pair of constrained masses
as a unit.
Let's use this approach to replace the distinction
bewteen gravitational and inertial mass, just to see
how it looks.
The accelerating force is provided by the weight W2
of m2 which is given by
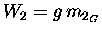 ,
where m2G
is the gravitational mass of m2. However, this force must accelerate
both objects at the same rate because the string constrains
both to move together (though in different directions).
Thus the net inertia to be overcome by W2 is the sum
of the inertial masses of m1 and m2, so the acceleration
is given by
,
where m2G
is the gravitational mass of m2. However, this force must accelerate
both objects at the same rate because the string constrains
both to move together (though in different directions).
Thus the net inertia to be overcome by W2 is the sum
of the inertial masses of m1 and m2, so the acceleration
is given by
The latter form expresses the acceleration explicity in units of
g, the acceleration of gravity, which is often called "one gee."
Suppose we have three identical objects,
each of which has the same inertial mass
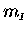 and the same gravitational mass
and the same gravitational mass
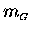 .
[This can easily be checked
using a balance and a standard force like a spring.]
Then we use two of them for m1 and m2,
set the apparatus in motion and measure the acceleration in "gees."
The result will be
.
[This can easily be checked
using a balance and a standard force like a spring.]
Then we use two of them for m1 and m2,
set the apparatus in motion and measure the acceleration in "gees."
The result will be
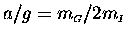 .
Next we put two of the objects on the cart
and leave the third hanging. This time we should get
.
Next we put two of the objects on the cart
and leave the third hanging. This time we should get
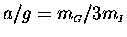 .
Finally we hand two and leave one on the cart,
for
.
Finally we hand two and leave one on the cart,
for
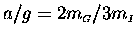 .
If the measured accelerations are actually
in the ratios of
.
If the measured accelerations are actually
in the ratios of
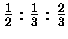 then it must be true that
then it must be true that
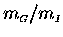 is constant - i.e.
that
is constant - i.e.
that
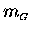 is proportional to
is proportional to
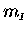 or that in fact they
are really basically the same thing (in this case)!
Unfortunately we have only confirmed this
for these three identical objects.
In fact all we have really demonstrated is that our original
postulates are not trivially wrong.
To go further we need to repeat the Eötvös experiment.
or that in fact they
are really basically the same thing (in this case)!
Unfortunately we have only confirmed this
for these three identical objects.
In fact all we have really demonstrated is that our original
postulates are not trivially wrong.
To go further we need to repeat the Eötvös experiment.


Up: The Free Body Diagram
Previous: The Free Body Diagram
Jess H. Brewer -
Last modified: Fri Nov 13 17:33:33 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE 

![]() ,
where m2G
is the gravitational mass of m2. However, this force must accelerate
both objects at the same rate because the string constrains
both to move together (though in different directions).
Thus the net inertia to be overcome by W2 is the sum
of the inertial masses of m1 and m2, so the acceleration
is given by
,
where m2G
is the gravitational mass of m2. However, this force must accelerate
both objects at the same rate because the string constrains
both to move together (though in different directions).
Thus the net inertia to be overcome by W2 is the sum
of the inertial masses of m1 and m2, so the acceleration
is given by
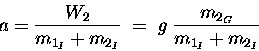
![]() and the same gravitational mass
and the same gravitational mass
![]() .
[This can easily be checked
using a balance and a standard force like a spring.]
Then we use two of them for m1 and m2,
set the apparatus in motion and measure the acceleration in "gees."
The result will be
.
[This can easily be checked
using a balance and a standard force like a spring.]
Then we use two of them for m1 and m2,
set the apparatus in motion and measure the acceleration in "gees."
The result will be
![]() .
Next we put two of the objects on the cart
and leave the third hanging. This time we should get
.
Next we put two of the objects on the cart
and leave the third hanging. This time we should get
![]() .
Finally we hand two and leave one on the cart,
for
.
Finally we hand two and leave one on the cart,
for
![]() .
If the measured accelerations are actually
in the ratios of
.
If the measured accelerations are actually
in the ratios of
![]() then it must be true that
then it must be true that
![]() is constant - i.e.
that
is constant - i.e.
that
![]() is proportional to
is proportional to
![]() or that in fact they
are really basically the same thing (in this case)!
Unfortunately we have only confirmed this
for these three identical objects.
In fact all we have really demonstrated is that our original
postulates are not trivially wrong.
To go further we need to repeat the Eötvös experiment.
or that in fact they
are really basically the same thing (in this case)!
Unfortunately we have only confirmed this
for these three identical objects.
In fact all we have really demonstrated is that our original
postulates are not trivially wrong.
To go further we need to repeat the Eötvös experiment.