BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

Momentum is Still Conserved!

For instance, MOMENTUM CONSERVATION must still hold, or else we would be able to tell one reference frame from another (in an absolute sense) by seeing which one got less than its share of momentum in a collision. To pursue this example, we invoke MOMENTUM CONSERVATION in a glancing collision between two identical billiard balls, as pictured in Fig. 24.1:

[Get ready to keep track of a lot of subscripts and primes! If you want to avoid the tedium of paying close attention to which quantity is measured in whose rest frame, skip to the formal derivation in terms of LORENTZ INVARIANTS and the 4-MOMENTUM . . . . ]

  

Figure: A glancing collision between two identical billiard balls of rest mass m, shown in the reference frame of ball B. Ball A barely touches ball B as it passes at velocity u, imparting a miniscule transverse velocity $v_{{\scriptscriptstyle B}_\perp}$ (perpendicular to the initial velocity of A) to ball B and picking up its own transverse velocity $v_{{\scriptscriptstyle A}_\perp}$ in the process. Primed quantities (like $v_{{\scriptscriptstyle A}_\perp}'$ and $v_{{\scriptscriptstyle B}_\perp}'$) are measured in A's reference frame, whereas unprimed quantities (like $v_{{\scriptscriptstyle A}_\parallel} = u$, $v_{{\scriptscriptstyle A}_\perp}$ and $v_{{\scriptscriptstyle B}_\perp}$) are measured in B's reference frame.

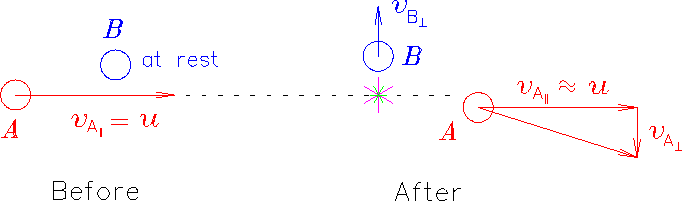Now, each of A and B is at rest in its own reference frame before the collision (A sees B approaching from the right at -u whereas B sees A approaching from the left at +u); after the collision, each measures^24.1 its own final velocity transverse (perpendicular) to the initial direction of motion of the other. Out of courtesy and in the spirit of scientific cooperation, each sends a message to the other reporting this measurement. By symmetry, these messages must be identical:

$$v'_{{\scriptscriptstyle A}_\perp} \; = \; v_{{\scriptscriptstyle B}_\perp}$$ (24.1)

Using the same argument, each must report the same measurement for the transverse component of the other's velocity after the collision:

$$v_{{\scriptscriptstyle A}_\perp} \; = \; v'_{{\scriptscriptstyle B}_\perp}$$ (24.2)

Meanwhile, MOMENTUM CONSERVATION must still hold for the transverse components in each frame:

$$\hbox{\rm In $B$\space (unprimed) frame} \qquad m \, v_{{\s . . . . . . m_{\scriptscriptstyle A} \, v_{{\scriptscriptstyle A}_\perp}$$ (24.3)

$$\hbox{\rm and in $A$\space (primed) frame} \quad m'_{\scrip . . . . . . e B}_\perp} \; = \; m \, v'_{{\scriptscriptstyle A}_\perp} ,$$ (24.4)

where the masses of the billiard balls in their own rest frames are written as m but I have expressly allowed for the possibility that a ball's effective mass in the other ball's frame may differ from its rest mass. (It helps to know the answer.) Thus $m_{\scriptscriptstyle A}$ is the effective mass of A as seen from B's reference frame and $m'_{\scriptscriptstyle B}$ is the effective mass of B as seen from A's reference frame.

We may now apply the LORENTZ VELOCITY TRANSFORMATION to the transverse velocity component of A:

$$v'_{{\scriptscriptstyle A}_\perp} \; = \; { v_{{\scriptscri . . . . . . - u^2/c^2 } \; = \; \gamma \, v_{{\scriptscriptstyle A}_\perp}$$ (24.5)

Combining Eq. (1) with Eq. (3) gives $m \, v'_{{\scriptscriptstyle A}_\perp} \; = \; m_{\scriptscriptstyle A} \, v_{{\scriptscriptstyle A}_\perp}$ which, combined with Eq. (5), gives $m \, \gamma \, v_{{\scriptscriptstyle A}_\perp} \; = \; m_{\scriptscriptstyle A} \, v_{{\scriptscriptstyle A}_\perp}$ or $m_{\scriptscriptstyle A} \; = \; \gamma \; m$. Similarly, combining Eq. (2) with Eq. (4) gives $m'_{\scriptscriptstyle B} \, v_{{\scriptscriptstyle A}_\perp} \; = \; m \, v . . . . . . criptstyle A}_\perp} \; = \; m \, \gamma \, v_{{\scriptscriptstyle A}_\perp}$or $m'_{\scriptscriptstyle B} \; = \; \gamma \; m$.

We can express both results in a general form without any subscripts:

$$m' \; = \; \gamma \, m$$ (24.6)

4.5inThe EFFECTIVE MASS m' of an object moving at a velocity $u = \beta c$ is $\gamma$ times its REST MASS m (its mass measured in its own rest frame). That is, moving masses have more inertia!