


Next: 3.2.1 The Raw Asymmetry
Up: 3 The SR Technique
Previous: 3.1 SR vs. NMR
In a 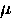 SR experiment,
positively charged muons are implanted
one at a time into the bulk of the superconductor.
The muon is a lepton which has spin 1/2, a rest mass
that is 206.729
times that of an electron, and a magnetic moment of
SR experiment,
positively charged muons are implanted
one at a time into the bulk of the superconductor.
The muon is a lepton which has spin 1/2, a rest mass
that is 206.729
times that of an electron, and a magnetic moment of
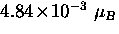 .In the cuprates the muon
comes to rest at a definite position in the crystallographic
unit cell--becoming hydrogen bonded to an oxygen atom [45].
Fortunately, in magnetic fields appropriate for a
.In the cuprates the muon
comes to rest at a definite position in the crystallographic
unit cell--becoming hydrogen bonded to an oxygen atom [45].
Fortunately, in magnetic fields appropriate for a 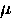 SR experiment,
the intervortex
spacing is much larger than the dimensions of the crystallographic unit cell
(typically 102-103 times larger)
so that a muon stops randomly on the length scale of the vortex lattice.
The implanted muon precesses about the local magnetic field B
with a Larmor frequency
SR experiment,
the intervortex
spacing is much larger than the dimensions of the crystallographic unit cell
(typically 102-103 times larger)
so that a muon stops randomly on the length scale of the vortex lattice.
The implanted muon precesses about the local magnetic field B
with a Larmor frequency
| 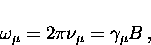 |
(4) |
where 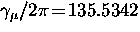 MHz/T is the muon gyromagnetic ratio.
After a mean lifetime
MHz/T is the muon gyromagnetic ratio.
After a mean lifetime 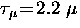 s, the positive muon decays
into a positron and two neutrinos (i.e.
s, the positive muon decays
into a positron and two neutrinos (i.e. 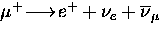 ).
The distribution of decay positrons is asymmetric with respect to the
spin polarization vector
).
The distribution of decay positrons is asymmetric with respect to the
spin polarization vector 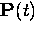 of the muon, where the highest
probability of emission is along the direction of the muon spin.
Consequently, the time evolution of the muon spin polarization
of the muon, where the highest
probability of emission is along the direction of the muon spin.
Consequently, the time evolution of the muon spin polarization
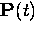 can be monitored,
since the muon partially reveals its spin direction at the time of decay.
can be monitored,
since the muon partially reveals its spin direction at the time of decay.
Scintillation detectors placed around the sample
can be used to detect the positrons emerging from the muon decay.
Figure 3.1 shows a simple four-counter arrangement.
The number of decay positrons recorded per time bin
 in the ith counter is given by
in the ith counter is given by
| ![\begin{displaymath}
N_{i}(t) = N_{i}^{\circ}e^{-t/ \tau_{\mu}} \left[ 1+A_{i}^{\circ}
\, P_{i}(t) \right] + B_{i}^{\circ} \, ,\end{displaymath}](img221.gif) |
(5) |
where 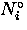 is a normalization
constant,
is a normalization
constant, 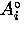 is the maximum precession amplitude,
is the maximum precession amplitude,
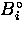 is a time-independent random background
and Pi(t) is the time evolution of the muon spin polarization
component in the ith direction, which is given by
is a time-independent random background
and Pi(t) is the time evolution of the muon spin polarization
component in the ith direction, which is given by
| 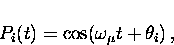 |
(6) |
where 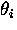 is the initial phase of the muon spin polarization vector
relative to the ith direction.
Generally
is the initial phase of the muon spin polarization vector
relative to the ith direction.
Generally 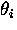 is nonzero, since the muons will precess
during their flight through the magnetic field to the sample.
There is no significant loss of polarization
during the short time over which the muons thermalize. This is because
the primary interactions by which the muons rapidly lose their initial
kinetic energy are electrostatic in nature and hence do not affect the
muon spin [46].
is nonzero, since the muons will precess
during their flight through the magnetic field to the sample.
There is no significant loss of polarization
during the short time over which the muons thermalize. This is because
the primary interactions by which the muons rapidly lose their initial
kinetic energy are electrostatic in nature and hence do not affect the
muon spin [46].



Next: 3.2.1 The Raw Asymmetry
Up: 3 The SR Technique
Previous: 3.1 SR vs. NMR
![]() SR experiment,
positively charged muons are implanted
one at a time into the bulk of the superconductor.
The muon is a lepton which has spin 1/2, a rest mass
that is 206.729
times that of an electron, and a magnetic moment of
SR experiment,
positively charged muons are implanted
one at a time into the bulk of the superconductor.
The muon is a lepton which has spin 1/2, a rest mass
that is 206.729
times that of an electron, and a magnetic moment of
![]() .In the cuprates the muon
comes to rest at a definite position in the crystallographic
unit cell--becoming hydrogen bonded to an oxygen atom [45].
Fortunately, in magnetic fields appropriate for a
.In the cuprates the muon
comes to rest at a definite position in the crystallographic
unit cell--becoming hydrogen bonded to an oxygen atom [45].
Fortunately, in magnetic fields appropriate for a ![]() SR experiment,
the intervortex
spacing is much larger than the dimensions of the crystallographic unit cell
(typically 102-103 times larger)
so that a muon stops randomly on the length scale of the vortex lattice.
The implanted muon precesses about the local magnetic field B
with a Larmor frequency
SR experiment,
the intervortex
spacing is much larger than the dimensions of the crystallographic unit cell
(typically 102-103 times larger)
so that a muon stops randomly on the length scale of the vortex lattice.
The implanted muon precesses about the local magnetic field B
with a Larmor frequency
![]() in the ith counter is given by
in the ith counter is given by