![\begin{displaymath}A_{ij}(t) = \frac{ \left[ N_{i}(t)-B_{i}^{\circ}
\right] - \ . . .
. . . }^{\circ} \right]
+ \left[ N_{j}(t) - B_{j}^{\circ}
\right] }
\end{displaymath}](img252.gif) |
(17) |
Consider the pair of counters i and j in Fig. 3.11,
analogous to counters R and L respectively in Fig. 3.10.
In a real experiment
one can define the raw asymmetry
Aij (t) of the appropriately
paired histograms Ni (t) and Nj (t) defined by
Eq. (3.16) as [77]:
where
so that
The motivation behind introducing
Aij (t) is the elimination of the
muon lifetime (which is a well known quantity)
and the random backgrounds
![]() and
and
![]() .
In the ideal situation,
the two counters in question are identical
to one another so that the
.
In the ideal situation,
the two counters in question are identical
to one another so that the ![]() SR histograms recorded by each differ
only by an initial phase. Because the muons travel for some time in the
applied field before reaching the sample, their initial
direction of polarization at the time of arrival in the sample
is field dependent. However,
the difference in phase between histograms is due solely to the geometry
of the positron counters with respect to the sample.
This situation is illustrated in Fig. 3.11.
In the presence of a constant magnetic flux density B, the
time evolution of the
muon spin polarization vector
SR histograms recorded by each differ
only by an initial phase. Because the muons travel for some time in the
applied field before reaching the sample, their initial
direction of polarization at the time of arrival in the sample
is field dependent. However,
the difference in phase between histograms is due solely to the geometry
of the positron counters with respect to the sample.
This situation is illustrated in Fig. 3.11.
In the presence of a constant magnetic flux density B, the
time evolution of the
muon spin polarization vector
![]() is given in general by
is given in general by
| (22) |
| (23) |
| (24) |
| (25) |
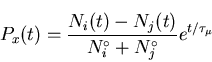 |
(28) |