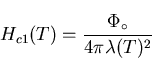 |
(20) |
As presented in their original form, the above results pertain almost
exclusively to type-I superconductors. The main topic of interest
here however, is the magnetic properties of type-II
superconductors, whose magnetization curve is depicted in Fig. 2.4.
Below Tc, in the presence of an externally applied magnetic
field H, three distinct phases are recognizable, dependent on the
strength of the applied field. Below a
lower critical field
Hc1 (T)the superconductor is in the Meissner state with full expulsion of
magnetic flux from its interior. For an applied
field above an upper critical field
Hc2 (T), magnetic flux fully penetrates the type-II material and
returns it to its normal state. Within Ginzburg-Landau theory, the lower
and upper critical fields may be written as:
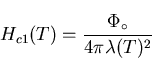 |
(20) |
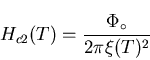 |
(21) |
If the applied field lies between
Hc1 (T)and
Hc2 (T), there is a partial penetration of flux into the sample leading
to regions in the interior which are superconducting and others which
are in the normal state; this is often referred to as the mixed state.
Ginzburg and Landau defined type-II superconductors as those with
![]() .
The high-temperature superconductors are extreme
type-II, with large GL parameters
.
The high-temperature superconductors are extreme
type-II, with large GL parameters ![]() (i.e.
(i.e.
![]() ),
large upper critical fields
Hc2 (T), and small lower critcal fields
Hc1 (T) [32,33,34].
),
large upper critical fields
Hc2 (T), and small lower critcal fields
Hc1 (T) [32,33,34].
In 1957, the Russian physicist Alexei A. Abrikosov predicted the existence
of type-II superconductors by considering the solution of the GL equations
for
![]() [35]. In particular, he considered
the case where the externally applied magnetic field H is only slightly
below
Hc2 (T); for in this region one obtains approximate solutions
resembling those of the linearized GL equations [13]. The
solutions revealed the presence of a periodic microscopic magnetic
field distribution, transverse to the applied field. More precisely his
efforts predicted a periodic square array of thin filaments of magnetic
flux in the mixed state. Consequently, literature sometimes refers to
the mixed state as the Abrikosov regime or for reasons to soon
be made apparent, the vortex state.
[35]. In particular, he considered
the case where the externally applied magnetic field H is only slightly
below
Hc2 (T); for in this region one obtains approximate solutions
resembling those of the linearized GL equations [13]. The
solutions revealed the presence of a periodic microscopic magnetic
field distribution, transverse to the applied field. More precisely his
efforts predicted a periodic square array of thin filaments of magnetic
flux in the mixed state. Consequently, literature sometimes refers to
the mixed state as the Abrikosov regime or for reasons to soon
be made apparent, the vortex state.
In the core region of a filament, the magnetic field is high and the
material does not superconduct here;
that is these regions are in the normal state. The
magnetic field is screened from the rest of the sample by supercurrents
which circulate around each filament. It is common to refer
to the filaments as vortex lines and the
array of filaments as a vortex lattice. At the vortex center where
the magnitude of the local field is largest, the density of superconducting
electrons ns and hence the order parameter
![]() is zero.
As one moves radially out from the center of a vortex core, nsincreases and the supercurrents screen a greater amount of flux. At a
radius on the order of the coherence length
is zero.
As one moves radially out from the center of a vortex core, nsincreases and the supercurrents screen a greater amount of flux. At a
radius on the order of the coherence length ![]() ,
ns approaches the value in the bulk of the sample. It follows
that the density of the supercurrents is greatest
near the edge of the vortex core where the
screening of the local magnetic field is at a maximum. Outside of the vortex
core, magnetic field leaks into the superconducting regions of the sample
( see Fig. 2.5), in much the same
way magnetic field penetrates the surface
of the semi-infinite
superconductor in Figure 1.2. The superconducting order parameter is, for all
intents and purposes, constant beyond regions of the order
,
ns approaches the value in the bulk of the sample. It follows
that the density of the supercurrents is greatest
near the edge of the vortex core where the
screening of the local magnetic field is at a maximum. Outside of the vortex
core, magnetic field leaks into the superconducting regions of the sample
( see Fig. 2.5), in much the same
way magnetic field penetrates the surface
of the semi-infinite
superconductor in Figure 1.2. The superconducting order parameter is, for all
intents and purposes, constant beyond regions of the order ![]() around
the vortex cores [36].
It may be noted here that
Abrikosov's prediction of the vortex state was remarkable in that it
precluded any concrete experimenital proof of its existence. He derived
the following relations between Hc1, Hc2, and the
thermodynamic critical field Hc:
around
the vortex cores [36].
It may be noted here that
Abrikosov's prediction of the vortex state was remarkable in that it
precluded any concrete experimenital proof of its existence. He derived
the following relations between Hc1, Hc2, and the
thermodynamic critical field Hc:
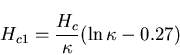 |
(22) |
| (23) |
In the dirty limit (
![]() ), one can write the upper critcal field
as [14]:
), one can write the upper critcal field
as [14]:
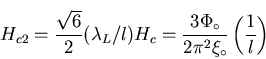 |
(24) |
One may wonder how London's magnetic penetration depth ![]() could be
incorporated into a theory for type-II superconductors. Although London's
original theory is indeed valid for
could be
incorporated into a theory for type-II superconductors. Although London's
original theory is indeed valid for
![]() ,
it makes no
mention of an upper critical field
Hc2 (T). Nevertheless, one
could anticipate some extension of the London model applicable to
type-II superconductors by consideration of specific features. To start
with, F. London theoretically predicted that magnetic flux is quantized
in a superconducting annulus. An analogous treatment of the supercurrents
that shield the vortex cores, leads one to deduce in several different
ways [13,17], that the flux associated with each vortex is
quantized and defined by:
,
it makes no
mention of an upper critical field
Hc2 (T). Nevertheless, one
could anticipate some extension of the London model applicable to
type-II superconductors by consideration of specific features. To start
with, F. London theoretically predicted that magnetic flux is quantized
in a superconducting annulus. An analogous treatment of the supercurrents
that shield the vortex cores, leads one to deduce in several different
ways [13,17], that the flux associated with each vortex is
quantized and defined by:
For an isolated vortex line, the field as determined in the extreme type-II
limit
![]() is [35]:
is [35]:
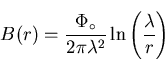 |
(27) |
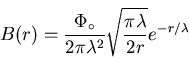 |
(28) |
The interaction between vortex lines becomes significant when their
separation is
![]() [38]. In a type-II superconductor,
the local magnetic field outside a vortex core decays in an exponential
manner so that one
is justified in describing the field in this region by the London
equations. In a crude sense, the mixed state of a type-II
superconductor may be visualized as a type-I superconductor with a
regular array of normal state regions (i.e. the vortex cores)
embedded in its interior. The magnetic penetration depth
[38]. In a type-II superconductor,
the local magnetic field outside a vortex core decays in an exponential
manner so that one
is justified in describing the field in this region by the London
equations. In a crude sense, the mixed state of a type-II
superconductor may be visualized as a type-I superconductor with a
regular array of normal state regions (i.e. the vortex cores)
embedded in its interior. The magnetic penetration depth ![]() is then
a measure of the length over which magnetic flux leaks into the
superconducting regions that encompass the vortex cores.
is then
a measure of the length over which magnetic flux leaks into the
superconducting regions that encompass the vortex cores.
The existence of the mixed state can be argued through free energy
considerations. Consider a sample in an applied magnetic field
Happlied with a normal phase and a superconducting phase separated by
a single interface. Realistically, the changeover between the two
phases is not abrupt. Magnetic field leaks into the
superconducting region a distance
![]() ,
resulting in a
contribution to the free surface energy of the interface that is negative.
In addition, the order parameter
,
resulting in a
contribution to the free surface energy of the interface that is negative.
In addition, the order parameter
![]() decreases to zero
over a distance
decreases to zero
over a distance ![]() ,
thereby decreasing the actual volume of
the sample which superconducts. This leads to a positive-energy
contribution at the interface. The sum of both phenomena give the
net surface energy per unit length at the interface as [39]:
,
thereby decreasing the actual volume of
the sample which superconducts. This leads to a positive-energy
contribution at the interface. The sum of both phenomena give the
net surface energy per unit length at the interface as [39]:
![\begin{displaymath}\sigma = \frac{1}{2} \mu_{\circ} H_{applied}^{2} \pi [\xi^{2} (T)
- \lambda^{2} (T)]
\end{displaymath}](img111.gif) |
(29) |
It has been argued
that the vortex model borne out of Abrikosov's solution of the
Ginzburg-Landau equations is the most energetically favourable form
for the magnetic flux to assume inside the superconductor [37].
Maximizing the surface-to-volume ratio of the normal regions leads
to the lowest energy situation in the mixed state, because this
provides the smallest positive surface-energy contribution. To achieve
this, one can form normal regions which constitute either lamina of
very small thickness (![]() )
or alternatively, filaments of small
diameter (
)
or alternatively, filaments of small
diameter (![]() ). Theoretical calculations indicate that the latter
formation is lowest in energy for
). Theoretical calculations indicate that the latter
formation is lowest in energy for
![]() [14].
[14].
Since Abrikosov's original prediction of a square vortex lattice, subsequent solutions of the GL equations for magnetic fields just below the upper critical field Hc2 (T), have convincingly shown that a periodic triangular array of vortex lines has the lowest free energy of all possible periodic solutions, and hence is the most stable configuration [13,40,41]. Decoration experiments which utilize small iron particles to make the vortices visible through an electron microscope have not only provided the best confirmation of the triangular arrangement but have also verified the flux quantum of Eq. (2.25) [42]. It is clear from such experiments which verify the flux quantum that it is energetically more favourable to increase the number of vortices as one increases the magnetic field, rather than increasing the amount of flux in each vortex [37]. Thus in an isotropic type-II superconductor, the vortex lines repel one another as a result of the magnetic force between them, to form an equilateral triangular lattice in accordance with energy minimization.