(Warning: Approx.
![]() is only accurate to
is only accurate to ![]() 13%!)
13%!)
- (a)
- If a mass m = 1 kg resting on a frictionless horizontal surface is attached to this ``spring,'' pulled out horizontally a distance of 10 cm from its equilibrium position and released from rest, plot the position as a function of time over the first full period of the motion. (Use numerical methods to approximate the motion by constant acceleration on small intervals, as in the free fall problem.)
- (b)
- Would the period be the same for a different amplitude of oscillation?
- (c)
- Would it be the same if the mass hung vertically from the ``spring'' in the Earth's gravity?
- (a)
- Show that the speed of a transverse wave in the rope
is a function of y, the distance from the lower end,
and is given by
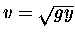 .
.
- (b)
- Show that the time it takes a transverse wave to
travel the length of the rope is given by
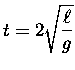 .
.