

Next: Gravity
Up: Old P120 Homework Questions
Previous: The Art of Estimating
- 1.
-
A basketball player, standing near the basket to grab a rebound, jumps
80
cm vertically. How much time does the player spend (a) in the top
20
cm of this jump and (b) in the bottom
20
cm? Does this help explain why such players seem to hang in the air
at the tops of their jumps?
- 2.
-
A juggler tosses balls vertically
0.8
m into the air. How much higher must they be tossed
if they are to spend twice as much time in the air?
- 3.
-
A stone is dropped into the water from a bridge
50 m
above the water. Another stone is thrown vertically down
0.8
s after the first is dropped.
Both stones strike the water at the same time.
(a) What was the initial speed of the second stone?
(b) Plot speed vs. time on a graph for each stone,
taking zero time as the instant the first stone was released.
- 4.
- At 12 noon, 1 Jan.
1988,
a radioactive sample exhibited
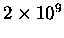 decays per second, emitting
decays per second, emitting 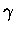 -rays.
It is known that there were 1017 atoms
of the radioactive species present,
arising from the calibrated dilution of a much larger sample.
How many decays per second did our sample exhibit at 12 noon,
20 Jan. 1990?
-rays.
It is known that there were 1017 atoms
of the radioactive species present,
arising from the calibrated dilution of a much larger sample.
How many decays per second did our sample exhibit at 12 noon,
20 Jan. 1990?
- 5.
- An object of mass
50
gm has density 19.3 gm/cm3. Here at UBC we watch it fall
inside a long vertical tube filled with a liquid of density
1.2
gm/cm3. We received this object from our friends in a space station.
They reported that they projected this object at an initial velocity of
1000
cm/s in a tank filled with the same kind of liquid; after traversing a
distance of 10 cm, travelling in a straight line,
it was moving at a velocity of 100 cm/s.
More detailed study showed that a linear drag force was indeed operating.
In our UBC experiment, what terminal velocity will we observe
for our object falling in the tube of liquid?


Next: Gravity
Up: Old P120 Homework Questions
Previous: The Art of Estimating