THE UNIVERSITY OF BRITISH COLUMBIA
Science 1 Physics
Assignment #
5:
Advanced Mechanics
Wed. 11 Oct. 2000 - finish by Wed. 18 Oct.
Figure:
: Superball
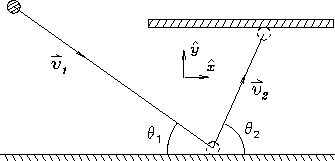 |
A ``superball'' is a hard rubber ball with a nearly perfect
coefficient of restitution and a huge coefficient of static
friction with hard, smooth surfaces. As a result, when it
bounces off such a surface we may treat the collision as
perfectly elastic (no loss of energy) and assume that
the point (of the ball) in contact with the surface during the
collision does not slip, no matter how acute the angle
 of its trajectory. To simplify the problem, we will
also assume that the following experiment is done in a
weightless environment, although the qualitative results
are unchanged by gravity.
of its trajectory. To simplify the problem, we will
also assume that the following experiment is done in a
weightless environment, although the qualitative results
are unchanged by gravity.
Figure:
: First Bounce:
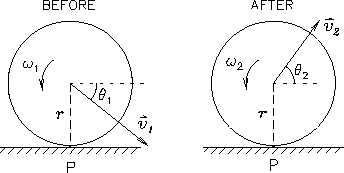 |
The ball is thrown at the floor with an initial velocity
 1
making an angle
1
making an angle 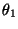 with the positive
with the positive 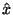 direction
or with the floor.1
The ball is not rotating initially (
direction
or with the floor.1
The ball is not rotating initially (
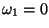 ).
After the collision we expect
).
After the collision we expect 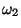 to be
negative.2
to be
negative.2
Assuming that the ball is a uniform solid sphere,
calculate the angle 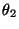 and the speed v2
in terms of
and the speed v2
in terms of 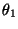 and
and
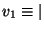
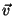 1|.
1|.
Under the Table:
If the ball was thrown under a table, as shown, with
the smooth, dry underside of the tabletop parallel
to the floor, show that it will always return
to the thrower's hand along the same trajectory it
followed in the first two bounces (shown in the figure).
Superball Design:
Does it matter if the ball is really a uniform solid sphere?
If it were a hollow sphere or a rubber sphere with a lead
centre, would you still obtain the same qualitative result?
What criteria are important? Explain.
. . . and
Tipler Ch. 8:
(4 Edition) problems
9, 86, 97 and 124
Edition) problems
9, 86, 97 and 124
. . . and Tipler Ch. 9:
(4 Edition) problems
5, 31, 53, 86 and 92
Edition) problems
5, 31, 53, 86 and 92

![]() and the speed v2
in terms of
and the speed v2
in terms of ![]() and
and
![]()
![]() 1|.
1|.
![]() Edition) problems
9, 86, 97 and 124
Edition) problems
9, 86, 97 and 124
![]() Edition) problems
5, 31, 53, 86 and 92
Edition) problems
5, 31, 53, 86 and 92