THE UNIVERSITY OF
BRITISH COLUMBIA
PHYSICS 455
Lecture # 9 :
Fri. 24 Jan. 1997
Guest Lecture by Brian Turrell:
Introduction to Ideal Gases
I. PARTICLE IN A BOX:
Using simple nonrelativistic quantum mechanics for a single particle
of mass M confined to a cubical box of side L and
volume V = L3 we can derive the
equation of state for an ideal gas:
Common sense dictates that if we have N truly non-interacting
particles together in the same box, each one will contribute equally to
the average thermal energy and the pressure, giving
U = (3/2) N  and p V = N
and p V = N  for the ideal gas. This turns out to be correct; in fact,
the equipartition theorem states that,
in the high temperature limit, a system will contain
for the ideal gas. This turns out to be correct; in fact,
the equipartition theorem states that,
in the high temperature limit, a system will contain
 /2 of energy
for each independent degree of freedom -
in the case of a monatomic gas, one for each of x, y and z
for each gas atom.
/2 of energy
for each independent degree of freedom -
in the case of a monatomic gas, one for each of x, y and z
for each gas atom.
However, students of quantum mechanics have learned not to rely too heavily
on the dictates of common sense. Moreover, there are some interesting
surprises when we try to decide whether the particles of the gas are
distinguishable or truly identical.
We shall therefore go through the transition from one particle to many
with some caution and rigour.
Last modified: Mon Feb 3 07:11:03 PST
 > =
|nx, ny, nz>
where the integer indices nx etc. are the numbers of
half-wavelengths in L in each direction.
> =
|nx, ny, nz>
where the integer indices nx etc. are the numbers of
half-wavelengths in L in each direction.

 =
= 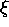 2
(nx2 +
ny2 +
nz2) where
2
(nx2 +
ny2 +
nz2) where
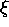 2
2 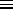 h2/8ML2 =
(h2/8M2) V-2/3.
h2/8ML2 =
(h2/8M2) V-2/3.
 ) unchanged
but will change the energy U1 =
) unchanged
but will change the energy U1 =

 .
We can thus use the first definition of the pressure to give
p1 = (2/3)
(h2/8M2) V-5/3
= (2/3) U1/V.
.
We can thus use the first definition of the pressure to give
p1 = (2/3)
(h2/8M2) V-5/3
= (2/3) U1/V.
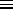 (2
(2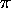
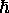 2 /
M
2 /
M )3/2
is the so-called quantum volume (a function of temperature)
which defines (roughly) the smallest volume to which a particle
can be confined and still have this treatment (based on a continuous
approximation to the density of states) be valid. The quantum volume
is (sort of) the volume of a cube one thermal de Broglie wavelength
on a side, where the thermal de Broglie wavelength is (within a slightly
ambiguous constant factor of order one) the de Broglie wavelength of a
nonrelativistic particle with a kinetic energy of
)3/2
is the so-called quantum volume (a function of temperature)
which defines (roughly) the smallest volume to which a particle
can be confined and still have this treatment (based on a continuous
approximation to the density of states) be valid. The quantum volume
is (sort of) the volume of a cube one thermal de Broglie wavelength
on a side, where the thermal de Broglie wavelength is (within a slightly
ambiguous constant factor of order one) the de Broglie wavelength of a
nonrelativistic particle with a kinetic energy of  .
We may alternatively define the single particle partition function
in terms of the quantum concentration
nQ
.
We may alternatively define the single particle partition function
in terms of the quantum concentration
nQ 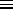 1/VQ
1/VQ 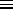 (M
(M /2
/2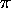
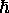 2)3/2
: Z1 = V nQ.
2)3/2
: Z1 = V nQ.
 2
2
 (log Z)/
(log Z)/
 to get U1 = (3/2)
to get U1 = (3/2)  .
.
 ,
the equation of state for a single particle in abox.
,
the equation of state for a single particle in abox.