 log
log  as an ``ENERGY OFFSET'':
as an ``ENERGY OFFSET'': LOGISTICS: Brian Turrell will take the Friday lecture this week, as I will be in Toronto at a CIAR meeting.
HANDOUTS: Assignment 4
READING: Finish up Ch. 3.
 log
log  as an ``ENERGY OFFSET'':
as an ``ENERGY OFFSET'':  > while in thermal equilibrium
with a heat reservoir at temperature
> while in thermal equilibrium
with a heat reservoir at temperature  is
P
is
P =
exp(-
=
exp(-
 /
/ )/Z
= exp(-
)/Z
= exp(-
 /
/ )
/ exp(-F/
)
/ exp(-F/ )
= exp(-[
)
= exp(-[
 - F]/
- F]/ ).
That is, if we measure energies relative to F (as a ``zero'' of energy)
then P
).
That is, if we measure energies relative to F (as a ``zero'' of energy)
then P requires no
normalization for the Boltzmann factor.
requires no
normalization for the Boltzmann factor.
This might look a little dangerous: if

 < F, we could get P
< F, we could get P > 1!
This can never happen, though, since Z is dominated by the smallest
> 1!
This can never happen, though, since Z is dominated by the smallest


 min:
Z = exp(-F/
min:
Z = exp(-F/ ) >
exp(-
) >
exp(- min/
min/ )
so F <
)
so F <  min
and therefore no
min
and therefore no

 can ever be smaller than F.
can ever be smaller than F.


A long skinny box (cross sectional area A and length x, so
volume V = A x) contains a particle in a certain quantum state
|  > for which there are nx
half-wavelengths in the length x and therefore a momentum in the x
direction given by px = h/
> for which there are nx
half-wavelengths in the length x and therefore a momentum in the x
direction given by px = h/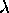 .
This produces a pressure p on the ends of the box. If one end moves
a distance dx under the force pA the work done on the particle
is dW = - p A dx = - p dV. In this process the wavelength gets longer
but the particle stays in the same state (though the state itself changes).
Thus there is no change of entropy in this process. All that changes
is the volume and the energy. Mathematically, dU =
(
.
This produces a pressure p on the ends of the box. If one end moves
a distance dx under the force pA the work done on the particle
is dW = - p A dx = - p dV. In this process the wavelength gets longer
but the particle stays in the same state (though the state itself changes).
Thus there is no change of entropy in this process. All that changes
is the volume and the energy. Mathematically, dU =
( U/
U/ V)
V) dV for such an adiabatic (isentropic) process.
dV for such an adiabatic (isentropic) process.
Comparing this with the work done on the particle (or a gas of independent,
non-interacting particles obeying the same rules) implies that p = -
( U/
U/ V)
V) which is (one of) the formal definition(s) of p:
the volume rate of change of energy at constant entropy.
which is (one of) the formal definition(s) of p:
the volume rate of change of energy at constant entropy.
 is a function only of
U and V. Thus
d
is a function only of
U and V. Thus
d =
(
=
(
 /
/ U)V
dU +
(
U)V
dU +
(
 /
/ V)U dV.
V)U dV.
If we specify constant entropy processes
(d = 0)
and recall the original definition of temperature
as well as the definition of pressure derived above, then we find
p =
= 0)
and recall the original definition of temperature
as well as the definition of pressure derived above, then we find
p =  (
(
 /
/ V)U,
an alternate definition of pressure.
V)U,
an alternate definition of pressure.
 and out equation reads d
and out equation reads d =
(1/
=
(1/ ) dU +
(p/
) dU +
(p/ ) dV.
This can be rearranged to give the differential form of the First Law
of Thermodynamics:
) dV.
This can be rearranged to give the differential form of the First Law
of Thermodynamics:
dU =
 d
d - p dV
- p dV
 d
d is the heat energy added to the system and
- p dV is the mechanical work done on the system.
You may recall having seen this before.
is the heat energy added to the system and
- p dV is the mechanical work done on the system.
You may recall having seen this before.

 :
:
Taking the exact differential yields
dF = dU -  d
d -
-  d
d =
=
 d
d - p dV -
- p dV -  d
d -
-  d
d or dF = -
or dF = -  d
d - p dV. That is, the free energy is constant in any
reversible process at constant temperature and volume.
- p dV. That is, the free energy is constant in any
reversible process at constant temperature and volume.
 =
=
 r(Ur)
+
r(Ur)
+  s(Us)
=
s(Us)
=  r(U)
- (1/
r(U)
- (1/ )Us
+
)Us
+  s(Us)
=
s(Us)
=  r(U)
- (1/
r(U)
- (1/ )Fs.
The first term on the right is a constant, and in equilibrium
)Fs.
The first term on the right is a constant, and in equilibrium
 must be a maximum, so
must be a maximum, so
F is always minimum in thermal equilibrium.
 d
d -
-  d
d =
=  d
d - p dV -
- p dV -  d
d -
-  d
d or
or
dF =
-  d
d - p dV
- p dV
 , the above relation
gives p = - (
, the above relation
gives p = - ( F/
F/ V)
V) ,
an alternate definition of pressure.
,
an alternate definition of pressure.
 =
- (
=
- ( F/
F/
 )V,
an alternate definition of entropy.
)V,
an alternate definition of entropy.
Note that the ``formula'' for the free energy,
F = -  log
log  ,
can be derived from the above definition of the entropy and the
thermodynamic definition of F using the expression for
the energy U in terms of a temperature derivative of log Z.
Check it for yourself.
,
can be derived from the above definition of the entropy and the
thermodynamic definition of F using the expression for
the energy U in terms of a temperature derivative of log Z.
Check it for yourself.
(
 /
/ V)
V) = (
= ( p/
p/
 )V
)V
p = -( U/
U/ V)
V) +
+  (
(
 /
/ V)
V)
 as a function of temperature.
as a function of temperature.
 in the Two-State System:
in the Two-State System:
We have Z = 1 + e- /
/ giving F = -
giving F = -  log(1 + e-
log(1 + e- /
/ )
From this and the definition of the entropy as the temperature derivative of F
at constant volume, we obtain (after a little calculus)
)
From this and the definition of the entropy as the temperature derivative of F
at constant volume, we obtain (after a little calculus)
 = log(1 + e-
= log(1 + e- /
/ )
+ (
)
+ ( /
/ ) /
(e
) /
(e /
/ ) + 1).
) + 1).

 0, as expected,
and levels off at log 2 (the maximum possible entropy for a 2-state system)
at high temperature, again as expected. Note that such limited systems
don't hold much heat energy!
0, as expected,
and levels off at log 2 (the maximum possible entropy for a 2-state system)
at high temperature, again as expected. Note that such limited systems
don't hold much heat energy!
 for the Harmonic Oscillator:
for the Harmonic Oscillator:
We have Z = 1/(1 -
e-
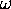 /
/ )
giving F =
)
giving F =  log(1 - e-
log(1 - e-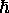
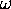 /
/ ).
Thus
).
Thus
 = - log(1 -
e-
= - log(1 -
e-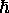
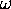 /
/ )
+ (
)
+ (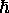
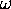 /
/ ) /
(e
) /
(e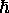
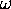 /
/ ) - 1).
) - 1).

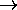 0, as expected,
but grows without limit as the temperature increases:
the higher the temperature, the more (higher energy) modes
can be involved, adding to the entropy.
0, as expected,
but grows without limit as the temperature increases:
the higher the temperature, the more (higher energy) modes
can be involved, adding to the entropy.
p = -( U /
U /
 V)
V) =
=  (
(
 /
/
 V)U
= -(
V)U
= -( F /
F /
 V)
V)
What we need now to do any practical calculations is a
specific result - a formula for p in terms of
N, V and  , for instance.
Such a relationship is called an equation of state.
On Friday Brian Turrell will introduce the most important one of all,
that for an ideal gas.
, for instance.
Such a relationship is called an equation of state.
On Friday Brian Turrell will introduce the most important one of all,
that for an ideal gas.