All this has been for a single SHO. A system of N
such independent oscillators will, on average, have just N times
the energy and heat capacity of one. A 3D version (e.g.
a simple crystal lattice) will have three vibrational degrees of freedom
(x, y and z) for each mass, giving a heat capacity
(dimensionless version) of 3N at high temperature.
Expressed in conventional units this would be 3N kB;
or, in terms of the heat capacity per mole, cV
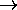 3R as
3R as 
 ,
where R
,
where R  No kB and No =
6.02.1023 is Avogadro's number.
No kB and No =
6.02.1023 is Avogadro's number.
This is known as the Law of Dulong & Petit
and describes the heat capacity of many solids quite well -
namely, those crystals which are built up from a basis
of dissimilar atoms which vibrate against each other at a well-defined
frequency  . (Such vibrations are known as
optical phonons because their frequencies are high, comparable
with infrared photons.) In simpler crystals
the lowest energy vibrational modes involve many atoms moving together,
the so-called ``acoustic phonon modes;''
we shall treat that case in some detail later on.
. (Such vibrations are known as
optical phonons because their frequencies are high, comparable
with infrared photons.) In simpler crystals
the lowest energy vibrational modes involve many atoms moving together,
the so-called ``acoustic phonon modes;''
we shall treat that case in some detail later on.
 = mB.
= mB.
 ).
).
 ) = -MB.
) = -MB.
 ).
).

 mB:
M = Nm2B/
mB:
M = Nm2B/ .
.

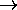 0 where
M
0 where
M 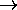 Nm.
However, the exact formula does reduce to the Curie law in the appropriate
high-temperature limit: as mB/
Nm.
However, the exact formula does reduce to the Curie law in the appropriate
high-temperature limit: as mB/
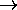 0,
exp(
0,
exp( mB/
mB/ )
)
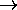 1
1  mB/
mB/ and
tanh(mB/
and
tanh(mB/ )
)  mB/
mB/ .
Thus M
.
Thus M  Nm2B/
Nm2B/ [Curie law].
[Curie law].

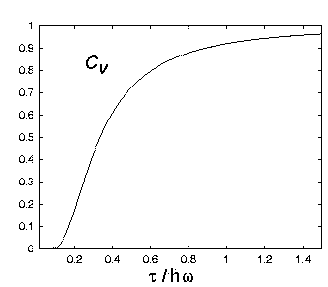
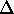
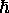
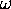 where
where
 1
to both increase monotonically with
1
to both increase monotonically with 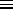
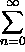 yn = 1/(1-y) or Z =
1/(1-exp[-
yn = 1/(1-y) or Z =
1/(1-exp[- (log Z)/
(log Z)/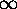 ,
indicating that new ``degrees of freedom'' (higher energy levels)
are thermally activated at a constant rate as the temperature increases.
,
indicating that new ``degrees of freedom'' (higher energy levels)
are thermally activated at a constant rate as the temperature increases.
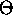 E
E