
 exp(-
exp(-
 /
/ )
)



 exp(-
exp(-
 /
/ )
=
)
=  2
2
 (log Z)/
(log Z)/


 exp(-
exp(-
 /
/ )
)



 exp(-
exp(-
 /
/ )
=
)
=  2
2
 (log Z)/
(log Z)/

 .
.
Then
Z = 1 + exp(- /
/ )
)
and U =  e-
e- /
/ .
/Z =
.
/Z =  /
(e
/
(e /
/ + 1)
+ 1)
 /2 and the upper state has an
energy of +
/2 and the upper state has an
energy of + /2.
/2.
Then
Z = exp(+ /2
/2 )
+ exp(-
)
+ exp(- /2
/2 )
= 2 cosh(
)
= 2 cosh( /2
/2 )
)
and U = -( /2)
tanh(
/2)
tanh( /2
/2 ).
).
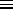 (
( U/
U/
 )V
for which we obtain in each of the two cases
)V
for which we obtain in each of the two cases
CV =
( /
/ )2
.
e
)2
.
e /
/ / (e
/ (e /
/ + 1)2.
+ 1)2.
LIMITING CASES:

 0:
0:
 /
/
 1 so
e
1 so
e /
/
 1, leaving
U
1, leaving
U 
 e-
e- /
/
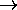 0 and
CV
0 and
CV 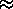 (
( /
/ )2
e-
)2
e- /
/
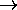 0 as well. (The exponential always grows or shrinks
faster than any power law.)
0 as well. (The exponential always grows or shrinks
faster than any power law.)

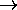
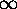 :
:
 /
/
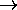 0 so
e
0 so
e
 /
/
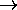 1
1 
 /
/ , giving
U
, giving
U 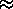
 /(2+
/(2+ /
/ )
)
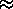
 /2
(i.e. no preference for either state) and
CV
/2
(i.e. no preference for either state) and
CV 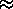 (
( /
/ )2
(1+
)2
(1+ /
/ ) /
(2+
) /
(2+ /
/ )2
)2
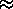 ½
(
½
( /
/ )2
)2
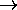 0.
(Once both states are equally populated, there is no place to put any more energy
on a statistical basis.)
0.
(Once both states are equally populated, there is no place to put any more energy
on a statistical basis.)