The way we do this is as follows: we assume U is only known (or specified) within some uncertainty dU and that dU (while very small) is much larger than the separation between any discrete energy levels in its range. We must then think of g(U) = D(U) dU in terms of the density of states D(U) per unit energy.
 of a system.
of a system.
 is a meaningful concept only for
predicting the most probable configuration
(how the energy gets shared) of two systems
in thermal contact. However, this can be very powerful!
is a meaningful concept only for
predicting the most probable configuration
(how the energy gets shared) of two systems
in thermal contact. However, this can be very powerful!
 (U)
somewhere in between.
At that value of U the inverse temperature
goes through zero.
(U)
somewhere in between.
At that value of U the inverse temperature
goes through zero.
 N
N -
N
-
N
 g(0,N)
exp(-2s2/N), valid for s
g(0,N)
exp(-2s2/N), valid for s
 N,
we can express the entropy in terms of the energy as
N,
we can express the entropy in terms of the energy as
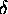 s1 / N1
at which g drops from its peak value gpeak
(defining the most probable configuration)
to [let us say] 1/e2
s1 / N1
at which g drops from its peak value gpeak
(defining the most probable configuration)
to [let us say] 1/e2 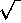 N1
if N1
N1
if N1