 g1
/
g1
/ U1
g2 + g1
U1
g2 + g1
 g2
/
g2
/ U1
U1
 > }
where the curly brackets denote ``the set of all...''
The number of different |
> }
where the curly brackets denote ``the set of all...''
The number of different |  >'s in the set
is the multiplicity g and the natural logarithm of g
is the entropy
>'s in the set
is the multiplicity g and the natural logarithm of g
is the entropy  .
This is about all the µCE is good for, except cocktail party
conversation (mystify your friends!) and defining the temperature:
.
This is about all the µCE is good for, except cocktail party
conversation (mystify your friends!) and defining the temperature:
0 =
 g1
/
g1
/ U1
g2 + g1
U1
g2 + g1
 g2
/
g2
/ U1
U1
(1/g1)
 g1
/
g1
/ U1
= (1/g2)
U1
= (1/g2)
 g2
/
g2
/ U2
U2

 1
/
1
/ dU1 =
dU1 =

 2
/
2
/ dU2
dU2

 /
/ dU.
We intuitively expect that two systems will stop exchanging heat
(except for small fluctuations) when they are at the same temperature,
so we should expect the derivative of the entropy with respect to the energy
to be equivalent to temperature.
dU.
We intuitively expect that two systems will stop exchanging heat
(except for small fluctuations) when they are at the same temperature,
so we should expect the derivative of the entropy with respect to the energy
to be equivalent to temperature.
Unfortunately this derivative has the opposite implication from what we
expect of temperature: the system with the higher

 /
/ dU
will tend to absorb heat from the system with the lower
dU
will tend to absorb heat from the system with the lower

 /
/ dU.
Because we have already gotten used to the idea that heat will
flow spontaneously from regions of high T to regions of low T,
we associate our derivative with the inverse temperature
dU.
Because we have already gotten used to the idea that heat will
flow spontaneously from regions of high T to regions of low T,
we associate our derivative with the inverse temperature
1/ =
=

 /
/ dU
dU
 are energy units.
If you really want to convert the entropy and temperature into
conventional units, use
are energy units.
If you really want to convert the entropy and temperature into
conventional units, use
S = kB  and
and
 = kB T
= kB T
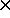 10-23
J/K is the Boltzmann constant.
10-23
J/K is the Boltzmann constant.
 - yes, one can, without too much trouble,
produce negative temperatures in the laboratory!
- yes, one can, without too much trouble,
produce negative temperatures in the laboratory!
Does this mean we can produce systems colder than absolute zero? Not at all. The inverse temperature is a smooth and monotonic function of U over the whole range of possible energies of the system, and it is just our insistence on adapting the theory to fit our conventions about ``high'' and ``low'' temperature that produce this nasty divergence. A negative infinite temperature is slightly hotter than a positive infinite temperature and the hottest temperature you can get is negative zero! If you need to predict the actual behaviour of thermal systems it is best to go back to the definition of thermal equilibrium.
Fortunately the exotic features of a spin system are only characteristic of closed systems with upper limits on energy, which we shall rarely encounter in physics elsewhere.
Insofar as an ideal socialist economy should redistribute any newly acquired (or created) wealth equally between all N members of society, there is only one microstate of the system and g = 1 no matter how much wealth the society possesses. By contrast, an ideal laissez-faire capitalist economy has all N members of society constantly striving to get a larger piece of the available U (wealth) and any new wealth added to the system will drastically increase the number of different ways it can be redistributed.
By our definitions, then,
 s = 0 and
s = 0 and
 c is an increasing
function of U, where the subscripts stand for socialist
and capitalist systems. Then
c is an increasing
function of U, where the subscripts stand for socialist
and capitalist systems. Then

 /
/ dU is always zero for the
socialist system and larger than zero for the capitalist system,
implying an infinite economic ``temperature'' for the former
and a finite one for the latter. What happens when a high-temperature
system is put in thermal contact with a low-temperature one? Hmm.
dU is always zero for the
socialist system and larger than zero for the capitalist system,
implying an infinite economic ``temperature'' for the former
and a finite one for the latter. What happens when a high-temperature
system is put in thermal contact with a low-temperature one? Hmm.
I propose that the most helpful thing the United States could possibly have done for Castro's Cuba was to try to isolate it economically. In the natural, random course of trade with Yankee money-grubbers, all the wealth in Cuba would have long ago trickled out into the USA and gotten lost in all the disorder, had the USA only welcomed Cuban traders with open arms. Not for any particular reason, of course, any more than there is a reason for heat to flow from a hot system to a cold one; there are just a lot more ways to be random when the temperatures are equal.
Enough sophistry. You decide for yourselves whether you think economic theory could benefit from the paradigms of Stat Mech. For now, let's get back to energy, entropy, temperature and physics.