- . . .
water).1
- Hint:
you must first find the pressure and density at that depth.
Look at sections 9.2, 9.2.1 and 9.2.9 in the textbook.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . \/.2
- This would be good for long-distance communication,
since lower frequencies are more weakly attenuated.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . that?3
-
The tone sf A has the frequency
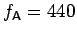 Hz.
One octave corresponds to a factor of 2 in frequency.
Each of the 12 semitones within one octave
differs from its neighbor by the frequency ratio 21/12.
For instance,
Hz.
One octave corresponds to a factor of 2 in frequency.
Each of the 12 semitones within one octave
differs from its neighbor by the frequency ratio 21/12.
For instance,
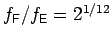 and
and
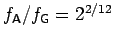 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . \/.4
-
This may seem rather short, but there are several reasons:
first, the lungs are not a fixed-volume container -
they are elastic, and the effective volume has been increased
to take this into account;
second, the "piston" air column is not the whole mouth and throat,
but just the region with the small area A specified -
which corresponds to a diameter of only about 1.4 cm,
which in turn is (not so surprisingly) about the same size
as our calculated L. The vibrating "mass on a spring"
is just the air between the baritone's teeth and lips.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . land.5
- Actually
this question could lead to a nice project:
How do they make the sound (PHYSICS),
and why do they do it (ZOOLOGY)?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.