Consider a human biceps as shown below.
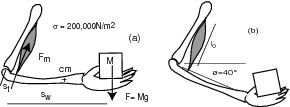
- Measure your biceps length
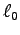 and the distance sw.
Estimate the distance st (explain how you do this).
Determine your muscle contraction
and the distance sw.
Estimate the distance st (explain how you do this).
Determine your muscle contraction 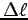 from similar triangles
from similar triangles
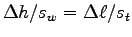 when moving the hand between positions (a) and (b).
Does the maximum contraction agree with the often quoted value
when moving the hand between positions (a) and (b).
Does the maximum contraction agree with the often quoted value
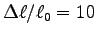 %?1 Determine the average cross sectional area and length
of your biceps muscle to find its volume
%?1 Determine the average cross sectional area and length
of your biceps muscle to find its volume 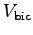 and mass
and mass
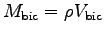 .
What value should you use for the muscle density
.
What value should you use for the muscle density 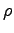 ?
ANSWER:
To measure
?
ANSWER:
To measure 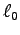 , make an angle of 90
, make an angle of 90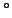 between your upper arm and forearm
and measure from the center of your shoulder down to the forearm.
To measure st (the distance from the back of the elbow
to where the biceps is attatched),
flex your biceps in the same position
and you will see where it attaches to the forearm.
From this point to the center of your elbow is st,
with which you can determine the leverage,
knowing the length sw of your forearm,
measured from the center of your hand to the elbow.
between your upper arm and forearm
and measure from the center of your shoulder down to the forearm.
To measure st (the distance from the back of the elbow
to where the biceps is attatched),
flex your biceps in the same position
and you will see where it attaches to the forearm.
From this point to the center of your elbow is st,
with which you can determine the leverage,
knowing the length sw of your forearm,
measured from the center of your hand to the elbow.
To measure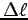 , hold your upper arm vertical
and lower your forearm until it makes
a 40
, hold your upper arm vertical
and lower your forearm until it makes
a 40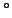 angle with the horizontal.
Still holding your upper arm vertical,
now raise your forearm until it is horizontal.
Note the change of height
angle with the horizontal.
Still holding your upper arm vertical,
now raise your forearm until it is horizontal.
Note the change of height 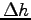 of the center of your hand
(the same point used in your sw measurement).
From the similar triangles rule you get
of the center of your hand
(the same point used in your sw measurement).
From the similar triangles rule you get
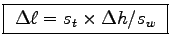 .
The oft-stated ratio is frequently an underestimate;
most people find a ratio
.
The oft-stated ratio is frequently an underestimate;
most people find a ratio
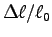 of between 10 and 15 %.
(Note also that this calculation includes tendons
in the total length
of between 10 and 15 %.
(Note also that this calculation includes tendons
in the total length 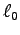 , so the muscle
must have an even larger fractional contraction!)
, so the muscle
must have an even larger fractional contraction!)
To determine the cross section of your biceps, measure its diameter d at its widest point when relaxed. As a first approximation you can model your biceps as two cones which are attatched on the flat side: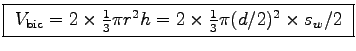 .
For the density of your muscle you can use
the density of water (
.
For the density of your muscle you can use
the density of water (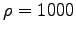 kg/m3).
kg/m3).
- Find a heavy weight, say M = 5-10 kg,
lift it as quickly as you can n = 10 times,2 and record the time
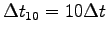 for these 10 cycles.
Estimate the average time
for these 10 cycles.
Estimate the average time 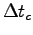 that the muscle spent
contracting in each cycle,
determine your normalized muscle contraction speed
that the muscle spent
contracting in each cycle,
determine your normalized muscle contraction speed
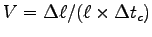 ,
and compare it to the normalized maximum power speed
,
and compare it to the normalized maximum power speed
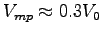 [s-1],
where V0 is the intrinsic muscle velocity for humans.3 Comment on the result.
ANSWER:
You can determine V exactly as stated in the question.
The textbook gives V0 = 3 s-1.
If you use this value you will get a value of Vmp
which usually does not fully agree with your contraction speeds.
One reason is that V0 is an avereage for humans;
some can contract faster, others much slower.
Another important factor is whether or not your
muscles "max out" (run out of available ATP)
during the repeated lifting.
[s-1],
where V0 is the intrinsic muscle velocity for humans.3 Comment on the result.
ANSWER:
You can determine V exactly as stated in the question.
The textbook gives V0 = 3 s-1.
If you use this value you will get a value of Vmp
which usually does not fully agree with your contraction speeds.
One reason is that V0 is an avereage for humans;
some can contract faster, others much slower.
Another important factor is whether or not your
muscles "max out" (run out of available ATP)
during the repeated lifting.
Determine the power needed to raise the weight: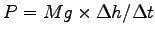 .
Estimate the mass ma of your forearm
and the approximate position of its center of mass (cm),
so that you can get estimates of the force Fa
and power Pa needed to move the forearm.
Add the forces Fm = F + Fa
and the powers Pm = P + Pa
and give estimates of the specific muscle force f = Fm/A
and the specific muscle power of your biceps p = Pm/ma.
.
Estimate the mass ma of your forearm
and the approximate position of its center of mass (cm),
so that you can get estimates of the force Fa
and power Pa needed to move the forearm.
Add the forces Fm = F + Fa
and the powers Pm = P + Pa
and give estimates of the specific muscle force f = Fm/A
and the specific muscle power of your biceps p = Pm/ma.
Make a table of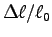 , ma,
contraction frequency
, ma,
contraction frequency
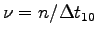 ,
V/V0, f and p for all team members.
,
V/V0, f and p for all team members.
ANSWER: Since you are told explicitly what to do there is no difficuly here, except for modeling of the forearm. The most elegant way to find its mass ma is the following: place a large bucket in an empty tray and fill the bucket exactly to the brim, until the first few drops of water overflow; then stick your forearm in the bucket and collect the resulting overflow in the tray. Measure the volume Vw of that water any way you like; it is the same as the volume Va of your forearm that displaced it. If this seems too messy, you can just use a round bucket only partly full and measure the height of the water in the bucket before and after bathing your arm. From the change in height and the diameter of the bucket you can find Va. Then use a density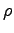 intermediate between that of bone and that of water
to calculate your forearm's mass
intermediate between that of bone and that of water
to calculate your forearm's mass
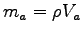 .
.
The center of mass is approximately in the center of your forearm (modeling it as a rod) as long as you are not a rock climber or weight lifter with extra strong forearms. In that case you could model it as a truncated cone, taking the diameter of your forearm where your biceps attaches as the base diameter and the diameter of your wrist as the truncation diameter. In general, the center of mass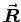 is defined by
is defined by
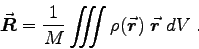
Now, we posed this problem in a form that allows you to neglect the "wasted" work done in accelerating and decelerating the weight and the forearm: this work would be the same if you did the experiment in a microgravity environment. To do that calculation you would need to know whether the rest of your body were fixed or free to move in reaction to the forces applied to the mass; and you would need to calculate the moments of inertia of the forearm plus weight to deterimine the rotational kinetic energy imparted in each motion. Fortunately, by using enough weight to make this a nearly "pure lifting" problem, we can avoid all that!
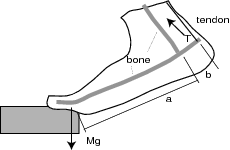
- Calculate the tension T in the Achilles tendon
of each member of your group when he or she stands
on the toes of one foot on a staircase, as shown above.
For that you will have to know the person's body mass M
and the relevant dimensions of their foot.
ANSWER:
First measure a and b, as indicated in the Figure.
You can assume that the axis of the tibia or "shin bone"
passes through the center of the large bump on your ankle,
and that the attachment point of the Achilles tendon
is half its diameter in from the back of your heel.
The ratio b/a is usually between 1/6 and 1/7.
If you are at rest, the downward gravitational attraction
of the Earth on your body (Mg) must be counteracted by
an equal and opposite upward force from the ground,
which is the reaction force to the downward force Mg
that your foot exerts on the ground, as shown in the Figure.
The force you must use to calculate the equilibrium of your foot
is, of course, the external upward force Mg
of the ground on your foot.
The Figure is a little misleading in this respect.
It is also misleading in showing the tibia at an angle;
this could only be the case if you were standing
in a crouched position, as when doing "squats" in the gym.
Normally your legs would be straight,
and therefore almost vertical -
and so would be the Achilles tendon.
If we treat the foot as a Free Body,
application of
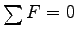 to yields
Mg + T = C, where C is the downward compression force
of the tibia on the foot, which is unknown.
We need more to solve the problem -
namely the condition for angular equilibrium,
to yields
Mg + T = C, where C is the downward compression force
of the tibia on the foot, which is unknown.
We need more to solve the problem -
namely the condition for angular equilibrium,
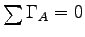 where the
where the 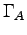 are
torques about some point A,
which we are free to choose anywhere we like.
It is almost always best to chose A somewhere along
the line of action of a force we don't need to know
(like C in the present case),
since that force produces no torque about that point.
So a good choice for A is the end of the tibia,
from which we measured a and b.
If we ignore the tilted tibia in the Figure,
we might also assume the foot itself to be horizontal,
so that all the forces are vertical and
act perpendicular to the horizontal "lever arm" of the foot.
This gives in one step
Mg x a = T x b or
are
torques about some point A,
which we are free to choose anywhere we like.
It is almost always best to chose A somewhere along
the line of action of a force we don't need to know
(like C in the present case),
since that force produces no torque about that point.
So a good choice for A is the end of the tibia,
from which we measured a and b.
If we ignore the tilted tibia in the Figure,
we might also assume the foot itself to be horizontal,
so that all the forces are vertical and
act perpendicular to the horizontal "lever arm" of the foot.
This gives in one step
Mg x a = T x b or
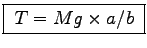 .
Interestingly,
if the foot makes an angle of
.
Interestingly,
if the foot makes an angle of 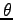 with the horizontal,
the result is unchanged! Why?
with the horizontal,
the result is unchanged! Why?
- Measure the radius r of each person's Achilles tendon and
determine the corresponding specific stress
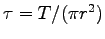 .
ANSWER:
Flex your calf muscles and you will see your Achilles tendon clearly.
Measure its diameter with a caliper, and subtract
your skin thickness (1-2 mm). Divide by two to get its radius.
The rest is self-explanatory.
.
ANSWER:
Flex your calf muscles and you will see your Achilles tendon clearly.
Measure its diameter with a caliper, and subtract
your skin thickness (1-2 mm). Divide by two to get its radius.
The rest is self-explanatory.
- Make a table of M, T and
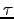 for all team members.
Email this information (in plain text, please!) to Alex
and he will make a compound table of this data for the whole class.
ANSWER: This is self-explanatory too.
for all team members.
Email this information (in plain text, please!) to Alex
and he will make a compound table of this data for the whole class.
ANSWER: This is self-explanatory too.
Air is a (mostly diatomic) molecular gas with specific heat
Cp = (7/2)R, where R = 8.31 J/mole![]() K
is the gas constant. Recall the Ideal Gas Law pV=nRT,
where the pressure p is in N/m2, the volume V is in m3,
n is the number of moles in the volume V
and the temperature T is always in
K
is the gas constant. Recall the Ideal Gas Law pV=nRT,
where the pressure p is in N/m2, the volume V is in m3,
n is the number of moles in the volume V
and the temperature T is always in ![]() K.
Differentiate the caloric energy equation,
K.
Differentiate the caloric energy equation,
![]() ,
to get the heat flow rate that must be provided by the lung
to maintain
,
to get the heat flow rate that must be provided by the lung
to maintain ![]() C.
C.
- How many moles are in one liter at this temperature and pressure?
How many moles per second does he inhale?
ANSWER:
The ideal gas law says pV = nRT,
where n is the number of moles and
R = 8.314472(15) J
 K
K mol-1 is the gas constant.
Thus n = pV/(RT). With
p = 1.03 x 105 N/m2,
T = 243 K and V = 10-3 m
mol-1 is the gas constant.
Thus n = pV/(RT). With
p = 1.03 x 105 N/m2,
T = 243 K and V = 10-3 m
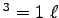 , we get
n1 = 0.0510 mol in one liter.
Bob takes in 6.0
, we get
n1 = 0.0510 mol in one liter.
Bob takes in 6.0  per minute (60 seconds),
so each second (on average) he breathes in
0.1
per minute (60 seconds),
so each second (on average) he breathes in
0.1  or
or
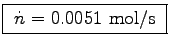 .
.
- How much heat power [Watts] does Robert lose by warming up the air?
ANSWER:
The specific heat of air (a diatomic gas, except for small impurities)
in this temperature range is
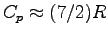 = 29.1 J
= 29.1 J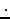 K
K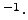 mol-1.
Thus
mol-1.
Thus
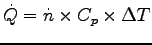 = 0.0051 x 29.1 x 66 or
= 0.0051 x 29.1 x 66 or
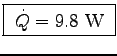 .
.
- What is the average intake velocity u
at which the air streams through his nostrils?
ANSWER:
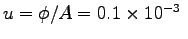 m3s
m3s
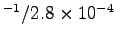 m2 or
m2 or
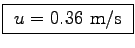 .
.
- Is the flow laminar (
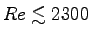 )
or turbulent (
)
or turbulent (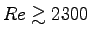 )?4 ANSWER:
Eq. (4.12) says
)?4 ANSWER:
Eq. (4.12) says
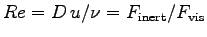 ,
the ratio of inertial to viscous forces, where
D is a typical dimension (like the diameter of a pipe),
u is a typical velocity and
,
the ratio of inertial to viscous forces, where
D is a typical dimension (like the diameter of a pipe),
u is a typical velocity and
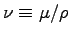 is the kinematic viscosity, which for air has a typical value
is the kinematic viscosity, which for air has a typical value
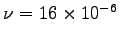 m2/s
(from Table 3.4 on p. 86 of the textbook).
If we treat Bob's notrils as circular,
an area of
2.8 x 10-4 m2
corresponds to a radius of
0.94 x 10-2 m
or a diameter
m2/s
(from Table 3.4 on p. 86 of the textbook).
If we treat Bob's notrils as circular,
an area of
2.8 x 10-4 m2
corresponds to a radius of
0.94 x 10-2 m
or a diameter
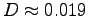 m.
Thus
m.
Thus
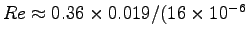 or
or
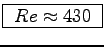 .
Therefore the flow is laminar,
which is extremly important!
Turbulent flow would be very inefficient
and it would cost Bob a lot of energy
to move oxygen into his lungs.
.
Therefore the flow is laminar,
which is extremly important!
Turbulent flow would be very inefficient
and it would cost Bob a lot of energy
to move oxygen into his lungs.
- Measure the open area A of your own nose
and provide this data along with the body mass for each individual.
Plot the area A as an allometric relation
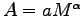 on a log - log graph for the members of your group.
What is the scaling exponent
on a log - log graph for the members of your group.
What is the scaling exponent 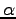 for your data?
What exponent do you expect? Why?
ANSWER:
Depends on your noses. ;-)
for your data?
What exponent do you expect? Why?
ANSWER:
Depends on your noses. ;-)
OK, seriously: according to the textbook (p. 151) the surface area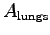 of the lungs
(which limits the amount of oxygen we can absorb)
scales as
of the lungs
(which limits the amount of oxygen we can absorb)
scales as
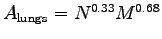 ,
where N is the number of alveoli,
which varies from person to person,
and M is (as usual) the body mass.
If we treat N as constant and assume simple geometrical scaling
of the volume V with the area
,
where N is the number of alveoli,
which varies from person to person,
and M is (as usual) the body mass.
If we treat N as constant and assume simple geometrical scaling
of the volume V with the area 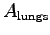 (
(
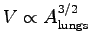 ),
this leads to a scaling of the volume of a human lung with body mass
as
V = 5.7 x 10-5 M1.03 [see Tenny and Remmer (1963) p. 150].
Assuming that the breath velocity u and time t per breath
are the same for everyone, the volume filled with air in one breath
should be V = u t A.
If we further assume that u t is the same for everyone,
then
),
this leads to a scaling of the volume of a human lung with body mass
as
V = 5.7 x 10-5 M1.03 [see Tenny and Remmer (1963) p. 150].
Assuming that the breath velocity u and time t per breath
are the same for everyone, the volume filled with air in one breath
should be V = u t A.
If we further assume that u t is the same for everyone,
then 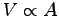 , which implies
, which implies
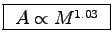 as well.
Of course, none of these assumptions are likely to be exactly right,
but this is the sort of reasoning we are looking for.
as well.
Of course, none of these assumptions are likely to be exactly right,
but this is the sort of reasoning we are looking for.